Neutron and gamma flux distributions and their implications for radiation damage in the shielded superconducting core of a fusion power plant

Colin G Windsor¹ and J Guy Morgan^2
1Tokamak Energy, D5, Culham Science Centre, Abingdon, OX14 3DB
²Culham Electromagnetics, D5, Culham Science Centre, Abingdon, OX14 3DB
E-mail: colin.windsor@tokamakenergy.co.uk

Abstract

The neutron and gamma ray fluxes within the shielded high-temperature superconducting central columns of proposed spherical tokamak power plants have been studied using the MCNP Monte-Carlo code. The spatial, energy and angular variations of the fluxes over the shield and superconducting core are computed and used to specify experimental studies relevant to radiation damage and activation. The mean neutron and gamma fluxes, averaged over energy and angle, are shown to decay exponentially through the shield and then to remain roughly constant in the core region. The mean energy of neutrons is shown to decay more slowly than the neutron flux through the shield while the gamma energy is almost constant around 2 MeV. The differential neutron and gamma fluxes as a function of energy are examined. The neutron spectrum shows a fusion peak around 1 MeV changing at lower energies into an epithermal E^-0.86 variation and at thermal energies to a Maxwellian distribution. The neutron and gamma energy spectra are defined for the outer surface of the superconducting core, relevant to damage studies. The inclusion of tungsten boride in the shield is shown to reduce energy deposition. A series of plasma scenarios with varying plasma major radii between 0.6 and 2.5 m was considered. Neutron and gamma fluxes are shown to decay exponentially with plasma radius, except at low shield thickness. Using the currently known experimental fluence limitations for high temperature superconductors, the continuous running time before the fluence limit is reached has been calculated to be days at 1.4 m major radius increasing to years at 2.2 m. This work helps validate the concept of the spherical tokamak route to fusion power by demonstrating that the neutron shielding required for long lifetime fusion power generation can be accommodated in a compact device.

PACS numbers: 52.55.Fa, 28.52.-s, 84.71.Ba

1. Introduction

Investigations with a system code have shown that the use of high temperature superconducting magnets in a spherical tokamak may allow an appreciable fusion gain with the comparatively low plasma major radius R₀=1.35 m [1]. Computations using the Monte Carlo code for N Particles [2,3] (MCNP Version 6.1) have shown that the superconducting column of such a tokamak might have a manageable heat deposition of order 50 kW [4,5] using a neutron shield of around 0.32 m thickness. However, there is concern that radiation damage of the superconductors may limit the lifetime of any such plant. At present, there is only limited experimental data on such damage [6], and the Vienna TRIGA Mark II reactor [7] used had a fission neutron spectrum not representative of a fusion reactor. Experimental HTS lifetime data with realistic neutron and gamma flux energy distributions, and the relevant cryogenic irradiation temperatures will not be easy to come by, and so flux calculations with associated radiation damage calculations may be the only available option for some time. The present studies predict the neutron and gamma ray energy spectra relevant to the radiation damage problem in the shielded superconducting core of a fusion plant.

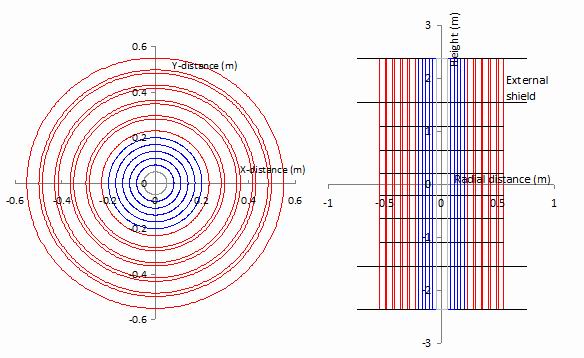
The simplified radial geometry of the spherical tokamak centre column used in the MCNP calculations is shown to the left in figure 1. In the centre is a cylindrical tie-rod of stainless steel and radius 0.05 m. Although the tie rod is divided into a further three surfaces of intermediate radius, these were not used for flux tallying. The high temperature superconductor core lies at radii between 0.05 m and 0.2 m. It is homogenised in composition and is divided into five annular volumes by the four cylindrical surfaces at intermediate radii shown in the figure. Between 0.2 m and 0.23 m radius is a vacuum gap inserted to make a thermal shield between the cryogenic column at around 20 K and the neutron shield at ambient temperatures. The neutron shield is at radii between 0.23 m and 0.55 m, and is made from five annular volumes each 0.052 m thick composed of a tungsten carbide or boride alloy, separated by four water channels each 0.015 m thick.

The vertical section to the right of figure1 shows how the central core and shield are divided by planes into 9 segments of unequal thickness detailed in [5]. The highest and lowest segments lie within the external shield.

Figure 1. The plan and vertical section of the geometry used showing the defining surfaces at which the fluxes have been calculated. The vertical scale has been compressed in the right-hand figure.

MCNP tracks the 14.1 MeV energy neutrons produced near the centre of the plasma and follows the neutrons, photons, protons and alpha particles produced by elastic scattering and inelastic reactions as a function of their spatial, angular and energy distributions. Here it is assumed that the neutrons are produced within a torus of elliptical cross section at a major radius of R₀=1.35 m with height +/- 0.14 m , and minor radius 0.0625 m. There is also an outer shield similar to the inner shield shown in figure 1 but with thickness 0.37 m, covering radii between 2.15 and 2.52 m. MCNP tracks the flux of each type of particle as they cross the various tally surfaces defined in the model. Here some 60 energy bins were used to define the flux distributions, ranging from thermal energies of 10 meV up to 25 MeV in roughly logarithmic intervals. In addition, fluxes are collected as a function of the angle at which the particles cross each surface. For most computations, just four angular tallies were used depending on the cosine of the angle q between the particle direction and the normal to the surface. Fluxes are described by MCNP in terms of the number of particles crossing the surface in the given angular and energy bins per source neutron created. Clearly this depends on the width of the energy bin, and the area of the surface. In this paper, fluxes will be described in units of neutrons per second, per square metre, per MeV. For a plant with 140 MW of neutron power, each neutron having an energy of 14.1 MeV or 2.26 x10^-12 joules, this would correspond to a neutron production rate of 6.19 x10¹⁹ neutrons per second.

In sections 2 to 8, two averaged properties are discussed: the energy and angle-integrated total flux through the shield, and the mean energy of the angle-integrated flux through the shield. Next the energy distributions are presented for both neutrons and gammas as a function of the position and nature of the shield. Lastly the angular distributions of the neutrons and gammas are detailed. Sections 9 and 10 deal with a new set of computations investigating the neutron and gamma flux distributions as a function of the plasma major radius for a set of operating conditions where the calculated maximum mechanical stress levels are roughly constant at an acceptable level. This enables the approximate lifetime of the superconducting core to be estimated as a function of the major radius.

2. The flux incident on the outside surface of the central column

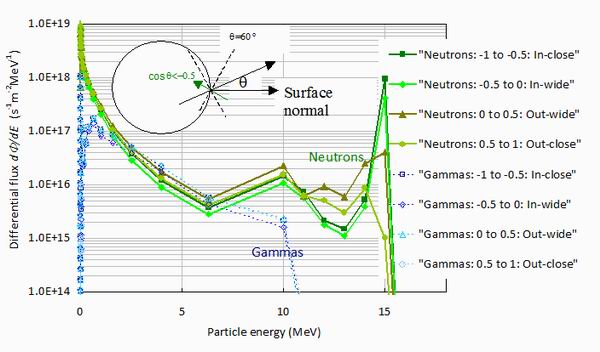
The central column is bounded by a cylindrical surface 0.55 m in radius. This surface records particles coming directly from the toroidal neutron source at 1.35 m radius, but also receives additional neutron and gamma ray fluxes from particles scattered by the outer shield and by particles scattered from within the central column. Figure 2 shows the neutron and gamma ray fluxes incident on the mid-plane sector of the central column at heights +/- 0.2 m as a function of energy for the four solid angle tallies. Particles entering the core have cosq <0 and those leaving it have cosq >0. Particles within 60⁰ of the normal to the surface have |cosq| >0.5 and those at wider angles than 60⁰ (which have the same solid angle) have |cosq| <0.5.

Figure 2. The neutron and gamma ray fluxes incident on the mid-plane sector of the central column at heights +/- 0.2 m on a log scale as a function of particle energy on a linear scale. The green upper full lines with closed symbols are the neutron fluxes for the ranges of the cosine of the angle to the normal shown. The lower blue dashed lines with open symbols are for gamma fluxes.

Figure 2 shows that for energies above 10 MeV the neutron flux is dominant, and that the 14.1 MeV fusion neutrons are mostly moving into the core, with much lower fluxes leaving the core, possibly having passed through it, or having been created within it. Around 12 MeV the situation has reversed and the flux leaving the core is higher as some of the incident 14.1 MeV neutrons are scattered back inelastically. At 11 MeV and below the neutron flux is essentially isotropic. The gamma ray flux is seen to be low at energies above 10 MeV but isotropic and to have a comparable or larger flux than the neutron spectrum at energies between around 1 and 7 MeV. The angular distributions will be investigated in more detail in section 8.

3. The height distribution of the central column flux

The central column was divided into 9 segments so that it is possible to determine the vertical dependence of the flux into the central column. The segments were defined in [5] and were not equal in height so the fluxes will be defined per m² of area. It is seen from figure 3 that the total neutron fluxes integrated over all energies into and out of the central core are comparable. The dashed lines in the figure show fits to the vertical distribution. This is seen to have a distribution lying between a Gaussian distribution with a full width at half height of 1.74 m, and a Lorentzian distribution with a full width of 1.47 m. The heavier dashed line shows the pseudo-Voigt function - a linear combination of Gaussian and Lorenzian distributions [8]. It is shown to give a good fit to the numerical profile with a full-width at half height of 1.58 m. It should be noted that these widths are rather lower than the good fit to a Gaussian distribution of full width 2.0 m suggested by the vertical distribution of deposited energy reported in reference [5]. In the remainder of this paper only the fluxes in the central mid-plane region of the core at height from -0.2 to 0.2 m where the fluxes are highest will be considered.

Figure 3. The neutron fluxes on to the outer layer of the central column as a function of vertical distance along the central column. The lower curves show the neutron fluxes from the plasma side into the core and out of the core and are seen to be almost equal. The total flux is well fitted by a pseudo-Voigt function between Gaussian and Lorenzian shapes with a full width at half height of 1.58 m.

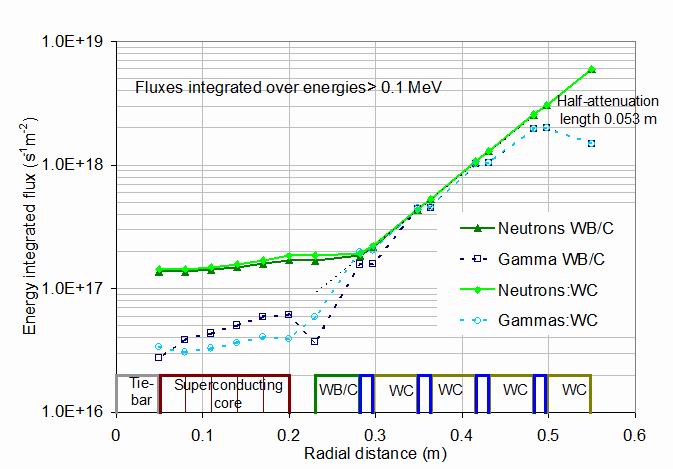
4. Energy-integrated neutron and gamma fluxes

Figure 4 shows the neutron and gamma fluxes for energies >0.1 MeV at various surfaces within the neutron shield and superconducting core. These layers are illustrated at the bottom of the figure. The neutron shield is composed of 5 layers of cemented tungsten carbide composite with an inner layer optionally of cemented tungsten boride. Between these are water-cooling layers. There is a thermal gap of 0.03 m between the shield and the superconducting core. Within this the superconducting core is measured at four intermediate surfaces as well as its inner and outer surfaces. Only results from the central mid-plane vertical section of the core where the fluxes are highest are shown. Figure 4 shows how the flux decreases through the neutron shield and becomes nearly constant over the superconducting core. The shield attenuation is roughly the same for neutrons and gammas and corresponds to a half-intensity attenuation distance of around 0.053 m as shown by the dashed line.

Figure 4. The neutron and gamma fluxes for energies over 0.1 MeV as a function of the radial distance through the core. The fluxes crossing each tally surface are given for neutrons and gammas and with either an all-tungsten carbide/water (WC) composite shield or one whose inner layer is composed of tungsten boride (WB/C) composite. The rectangles at the bottom of the figure indicate the various materials and their positions. The dashed line shows a half-intensity attenuation distance of around 0.053 m, which is followed generally through the shield for both neutrons and gammas.

For the boride-containing shield, the neutron flux >0.1 MeV in the superconducting layer is almost constant at around 1.5 x10¹⁷ s^-1m^-2. With the all tungsten carbide shield the neutron flux is around 20% higher and decreases slightly into the core. The gamma fluxes in the superconducting core are generally only around 20% of the neutron fluxes. The flux in the boride-containing shield, at around 6 x10¹⁶ s^-1m^-2 is around 30% higher than in the carbide shield. Each ¹⁰B neutron capture emits a gamma ray of 2.3 MeV energy, which may account for this. However, in the boride-containing layer itself the gamma flux is lower than with the all-carbide shield.

5. The mean neutron and gamma energies

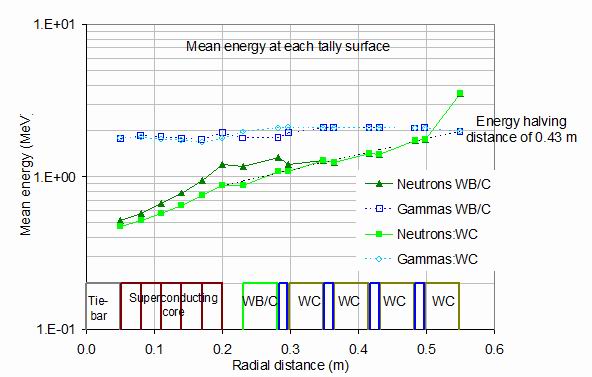
A second averaged figure of importance is the mean energy of neutrons and gammas as they pass through the shield and superconducting core. Figure 5 shows this for both tungsten carbide and water shields and for those containing an inner layer of tungsten boride.

For neutrons, the average energy drops significantly across the shield. On the outer plasma-facing surface the mean energy is 3.53 MeV, significantly lower than the fusion neutron energy of 14.1 MeV, as many neutrons are scattered by the surrounding outer shield. In the water layers of the shield there is little change in mean neutron energy, indeed, it sometimes rises slightly. For the all-tungsten carbide shield, after the first layer, there is a smooth reduction in mean energy across the rest of the shield. The dashed line in the figure corresponds to an energy-halving distance of 0.43 m. The mean energy of the neutrons within the boron-containing layer of the shield is increased by around 50% above that of the all tungsten carbide shield. This could represent the onset of appreciable neutron absorption by ¹⁰B as the lower energy neutrons are preferentially absorbed. In both shields the mean neutron energy continues to decrease with decreasing radius into the superconducting core and tie-bar.

Figure 5. The mean energy of the neutron and gamma fluxes as a function of the radial distance through the core. Results are shown for both an all-tungsten carbide composite shield and for one whose inner layer is composed of tungsten boride composite. The monitored surfaces are illustrated at the bottom of the figure.

The gamma energies in figure 5 are seen to be almost constant across the shield at around 2 MeV and almost identical between the all tungsten carbide and part boride shields. This is because the gammas are largely created by (n,g) reactions in tungsten. They have a cross section depending on energy but generally emit gammas with a range of energies centred around a few MeV. The result is that the average gamma energies are higher than the average neutron energies in all but the plasma-facing surface. Within the boride-containing layer the gammas are seen to have around 10% lower mean energy than in the all-carbide segment. This could be because the ¹⁰B (n,g) capture produces gammas of 2.31 MeV - rather lower than the mean energy from tungsten (n,g) capture.

6. The energy and radial dependences of the fluxes

The total fluxes of figure 4 need to be further examined to reveal the dependence of the neutron and gamma fluxes as functions of their energy. The flux F is expressed as the differential flux dq/dE per unit energy in MeV. This is necessary because the flux is divided into energy bins of unequal, approximately logarithmically varying width. With this definition, typical reactor neutron fluxes increase with decreasing energy, typically having the epithermal distribution nearly inversely proportional to the neutron energy from 1 MeV to around 100 eV, then changing to a Maxwellian distribution at thermal energies.

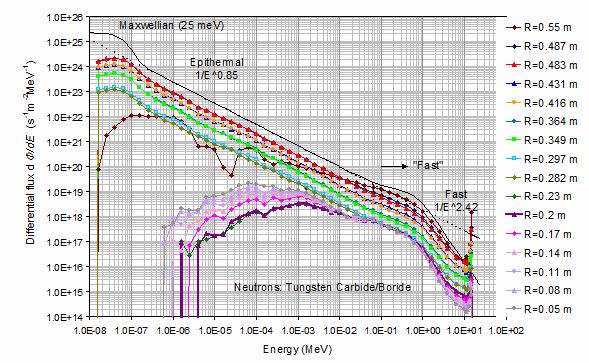
Figure 6. The neutron differential fluxes for a tungsten carbide and water shield with an inner layer of tungsten boride as a function of energy, for the radial surfaces defining the shield and superconducting core. The legend shows the radius of each tally surface, which can be correlated with the radial sections at the bottom of figures 4 and 5. The dark red diamonds show the outer plasma-facing surface. The orange and green lines correspond to surfaces in the shield, and the blue lines correspond to surfaces behind water layers. The heavy violet triangles indicate flux at the outer surface of the superconducting core, and the purple shaded lines below it the fluxes at the other tally surfaces within the core. The dashed line indicates an energy dependence in the differential flux 1/E^0.85 when E is the energy in MeV, and the full line a simulated Maxwellian distribution at thermal energies of 25 meV and including a fast neutron peak decaying with form 1/E^2.42.

Figure 6 shows these distributions for neutrons in the tungsten carbide and water shield. The energy scale goes from 10 meV, just below thermal energies, to well above the fusion neutron production energy of 14.1 MeV. The peak in the energy distribution near 14 MeV is clearly seen in the figure, and is maintained to some degree throughout the shield and superconducting core, since some fusion neutrons traverse the shield and core unscattered.

Over a broad range of energies from 0.1 MeV down to 0.25 eV there is an almost linear slope to the differential flux with an exponent E^-0.85, so slightly less steep than the epithermal 1/E energy distribution. At around 0.4 MeV the epithermal distribution changes into a broad fast neutron peak in the differential flux. This peak is maintained without much change in shape or relative amplitude at all the surfaces throughout the shield and core. This peak then decays at the high-energy end as 1/E^2.42. The full black line in the figure shows this fast neutron peak modelled by the function: dF/dE=AE^-0.85.T(E) +BE^-2.42[1-T(E)] , where A and B are amplitudes depending on the surface radius, and T(E) is a transfer function depending on the logarithm of the energy of form: T(E)=1/{1+exp[ln(E)-ln(E_T)]/ln(W_T)} where the transfer energy E_T and transfer width W_T are both about 0.7 MeV.

An exception to this distribution is the plasma-facing surface shown by the dark red diads. This occupies the top of the distributions above 0.01 MeV but its flux decays much faster with decreasing energy than the inner surfaces to reach a flux around that at the back of the neutron shield below 15 eV.

Around 25 meV a Maxwellian distribution replaces the epithermal energy dependences. In this distribution, the neutrons cease to lose energy on average, as they collide with atoms at thermal energies, assumed here to correspond to 300 K or about 25 meV. The Maxwellian distribution takes the form: dF/dE=F₀(E/kT)²*exp(-E/kT) where F₀ is the total flux integrated over all energies and is set equal to 10¹⁸ ns^-1m^-2 in the figure. It is interesting that there is no trace of a Maxwellian distribution at the outer surface of the shield (the dark red diamonds). Both sides of the outermost water layer show a clear Maxwellian contribution and this stays much the same until the boron-containing shield layer when it disappears completely.

The figure shows the differential flux in the water layers by blue tinted lines. These lie very close to the corresponding inner tungsten carbide surface and are difficult to distinguish except near the region around 0.4 MeV. This is consistent with the total fluxes shown in figure 4, which only dip slightly in the water layers.

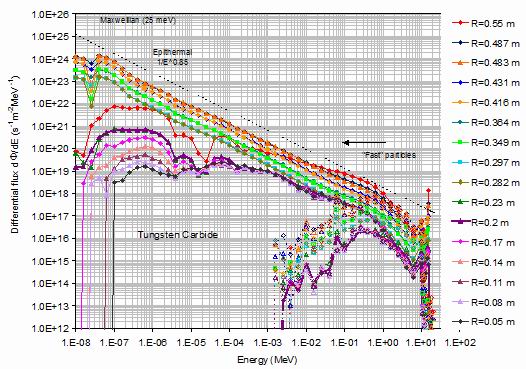
Figure 7. The figure shows the neutron (full lines and closed symbols) and gamma (dashed lines and open symbols) differential fluxes for the mixed tungsten carbide and water shield plotted as a function of energy for all the radial surfaces defining the shield and superconducting core. The heavy lines indicate the outer edge of the superconducting core. The dashed line shows an epithermal neutron distribution and the full line a Maxwellian corresponding to 25 meV thermal energies.

The outside surface of the superconducting core is shown by the heavy violet triangles and line. This line defines the maximum fast neutron flux seen by the superconducting core. It is seen that over an energy range from 1 MeV to 10 keV the surfaces within the superconducting core have closely similar fluxes. Below this energy, the differential flux rises slightly across surfaces inwards towards the centre of the superconducting core. This could be because of the increasing distance from the neutron absorbing boron layer. This effect is reversed in the all-tungsten carbide shield as shown in the following figure 7. However, this low energy range is of little significance for radiation damage.

Figure 7 shows the closely similar results for a shield composed of just tungsten carbide composite and water. Note that including the gammas, the vertical flux scale is extended to 100 times lower values. The neutron fluxes are very different in that the fluxes in the previously borated shield layer next to the core (shown in green) are very much larger. The neutron fluxes within the core extend to much lower energies and remain quite flat right down to thermal energies. The clear advantage of a borated shield layer is evident from the much lower thermal and epithermal neutron fluxes in figure 6 compared with figure 7. There is a sharp dip in the flux around 25 meV, not seen with the boride containing shield. The origin of this dip remains uncertain.

The gamma flux is shown by the dashed lines and open symbols with the same colours. It differs only slightly from the gamma flux in the tungsten boride-containing shield. While it is generally much lower than the neutron flux there is an energy range between 2 and 6 MeV when it is larger. The gamma flux attenuates rapidly below 1 keV and above 10 MeV and also drops rapidly to a value five orders of magnitude below its peak values around the MeV region. The forms of the spectra are quite different from the neutron spectra. They contain several distinct peaks at, for example, near 10 keV, 60 keV and 0.6 MeV. This time the water layers are almost identical to the outer carbide layer until below 10^-2 MeV, when the gamma flux is appreciably higher in the water layers.

Again, the fluxes crossing the outer surface of the superconducting core at a radius of 0.2 m are shown by the heavy violet lines. Other violet lines indicate surfaces within the superconducting core. In the case of neutrons for this shield it generally represents the largest flux seen in the core region with only a modest further reduction towards the centre of the superconducting core. In the case of gammas, the flux within the core is nearly constant.

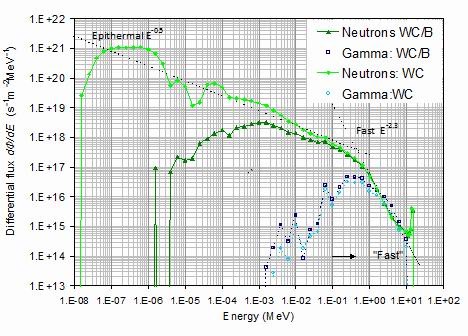
7. The flux distributions at the surface of the core

Figure 8 shows the neutron and gamma differential fluxes plotted just for the surface at radius 0.2 m defining the outside of the superconducting core. These are the surfaces shown by the violet lines in figures 6 and 7, but also include the all-tungsten carbide, boride and water shield results. These results define the nature of the radiation spectrum needed to test the lifetime of the high temperature superconducting tapes.

It is seen that the presence of the boride-containing layer next to the core makes a considerable difference in the neutron flux below 0.1 MeV. The difference increases as the energy is reduced and the boron absorption cross-section increases. With the boron-containing shield there is almost no flux below 1 eV.

In the case of the gamma flux it is seen that at energies below 1 MeV the neutron flux is higher than the gamma flux by an increasing ratio as the energy is reduced. However, over the range between 2 and 6 MeV the gamma flux is higher than the neutron flux. The inclusion of the boride-containing layer makes only a modest difference, however the boride increases the gamma flux by a factor increasing as the energy is reduced from about 5% at 0.1 MeV rising to a factor five at 0.004 MeV.

Figure 8. The neutron and gamma differential fluxes as a function of energy measured on the outer surface of the superconducting core at a radius of 0.2 m. The four curves are for neutrons and gammas and with either an all-tungsten carbide composite and water shield or one whose inner layer is composed of tungsten boride.

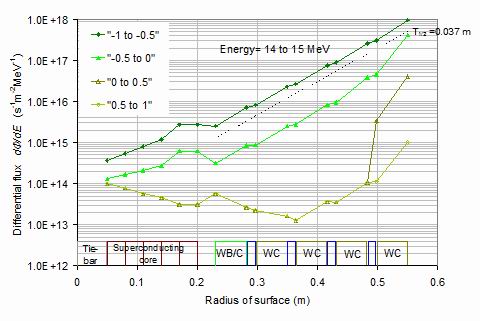
Figure 9. The angular dependences of the neutron differential flux between 14 and 15 MeV as a function of radial distance outwards from the centre of the superconducting core to the outer surface of the shield at a radius of 0.55 m for the shield containing a tungsten boride inner layer. It is seen that the 14.1 MeV fusion neutron anisotropy is maintained throughout the scan with the inwards flux being consistently higher than the outwards flux by an order of magnitude or more. The dashed line shows an intensity decrease into the shield halving in 0.037 m.

8. The angular dependences of the neutron and gamma fluxes

As mentioned in section 2 the flux computations have been further broken down into four angular ranges, inwards towards the core within 60⁰ of the normal, shown with cosθ as (-1 to -0.5), inwards at wider angle (-0.5 to 0), outwards at wider angle (0 to 0.5) and outwards at smaller angle (0.5 to 1). It is possible to follow the anisotropy of the differential flux as a function of radial position through the neutron shield. The energy range from 14 to 15 MeV includes the fusion neutrons. Figure 9 shows this energy range through a selection of the possible surfaces as a function of radius from the centre of the superconducting core. The inwards, close-angle, flux is always higher than the large-angle flux, and much higher that the outwards flux, which tends to be over 100 times lower near the centre of the shield. The gamma fluxes are negligible for this energy range.

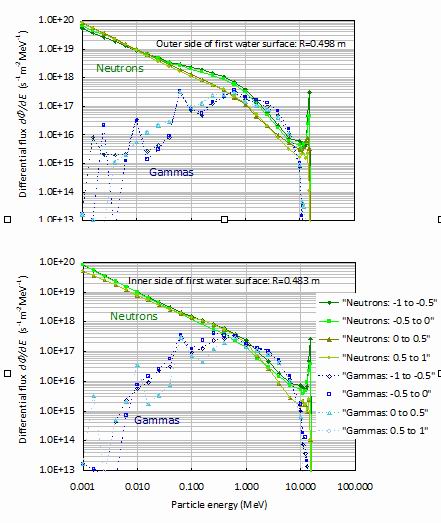
Figure 10. The angular dependences of the neutron and gamma differential fluxes as a function of energy measured for the two surfaces either side of the first water layer in the shield at (i) radius 0.498 m on the outside of the first water layer, and (ii) at 0.483 m on the inside of this layer. The sample had a tungsten carbide alloy and water shield with an inner layer of tungsten boride.

Figure 10 shows the differential flux as a function of energy and angle for (i) the outer side of the first water layer at 0.498 m, and (ii) the inner side of this water layer at 0.483 m. Several significant differences can be seen. Around the 0.1 to 1 MeV energy range the inwards neutron flux on the outside of the first water layer is around double than of the outward flux, but this difference is reduced to only about 50% for the inner side of the first water layer. This 1.5 cm thick water layer is therefore highly significant in making the neutron flux less directional. At epithermal energies below 0.1 MeV the flux is nearly isotropic in both cases.

In the case of the gammas, for example around 0.04 MeV, the inwards gamma flux is reduced by around a factor of three from the outside of the first water layer to the inside. However, the situation is reversed for the outwards gamma flux which is close to double the inwards flux on the inside of the first water layer. Clearly the gammas produced in the tungsten carbide pass into the water layer from both directions.

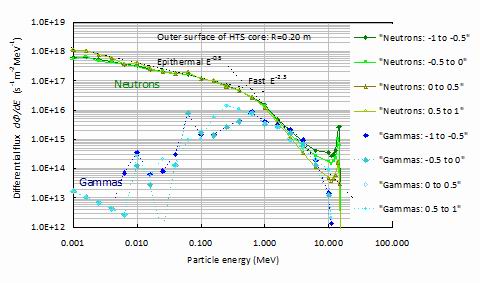
Figure 11 shows the angle dependent differential fluxes on the outer surface of the superconducting core. It is seen that while the neutron flux is largely isotropic below around 1 MeV, there remains considerable anisotropy in the flux distribution between around 4 MeV up to and including the fusion energy of 14.1 MeV where the two inwards fluxes are around an order of magnitude larger than the two outward fluxes.

The gamma fluxes are largely isotropic at energies down to 0.4 MeV but then develop considerable anisotropy with the outwards going flux being an order of magnitude larger than the inwards flux around 250 keV. At around 60 keV there is a distinct gamma peak due to neutron capture reactions in the shield, and the situation is reversed with the inwards flux being an order of magnitude higher.

Figure 11. The angular dependences of the neutron and gamma differential fluxes as a function of energy and direction, measured on the outer surface of the superconducting core at a radius of 0.2 m.

9. Neutron and gamma flux changes with plasma major radius

All the above computations have been for a fixed plasma major radius of 1.35 m. If it is essential to reduce the flux either because of excessive radiation damage to the superconductors, or because of too large a cryogenic heat load, one solution is to increase the plasma major radius. This increase is complicated by the fact that in any such radial scan there is wide choice of possible scans, depending on which variables are held constant. In the present work, the choice has been made to hold the fusion gain constant at 5, the aspect ratio constant at 1.8, and the I_PB98y2 H factor constant at 1.9. The central temperature was varied to give 0.8 of the Greenwald density limit and the toroidal field adjusted to give 0.9 of the beta limit. A further consideration is that the mechanical stresses in the tokamak must lie within acceptable limits. As described in [9], these conditions could be satisfied over a wide range of plasma major radii if the increased extra space made available by increasing the major radius is divided in the ratio 92% to the shield thickness and 8% to the HTS core radius. A series of 13 MCNP computations were made using this fraction from major radius R₀=0.592 m, where the shield thickness vanishes, to R₀=2.50 m where the shield thickness is 0.782 m. All runs include a constant vacuum gap of 0.015 m and a plasma wall gap of 0.025 m, which are half the thicknesses assumed in the earlier results presented here. No allowance has been made for the vacuum vessel thickness which would need to be included in a more realistic design. Table 1 shows a selection of parameters used in the present radial scan. Another difference is that the superconducting material extends into the region previously occupied by a steel tie-bar. The shield material was tungsten carbide composite and water without the presence of any boride.

R0 (m)	Pfus (MW)	Tcon (m)	Tshield (m)	BT (T)	Bcond (T)	Stress (Mpa)	q*	Psc (MW)	Pmc (MW)
0.5918	205.92	.223	0	7.449	19.766	312.543	4.832	15.5	8.83
0.6	205.85	.2233	.0033	7.365	19.787	313.208	4.824	14.7	8.7
0.625	205.65	.2242	.0001	7.12	19.847	315.131	4.801	12.4	8.09
0.65	205.46	.2251	.0238	6.893	19.902	316.883	4.778	10.5	7.55
0.7	205.11	.2269	.0442	6.482	19.997	319.919	4.734	7.52	6.47
0.9	203.84	.234	.126	5.257	20.22	327.083	4.576	1.98	2.14
1.1	202.61	.2411	.2078	4.443	20.268	328.622	4.442	.519	.568
1.35	201.03	.25	.31	3.736	20.176	325.657	4.298	.0977	.103
1.5	200.05	.2553	.3713	3.416	20.068	322.186	4.222	.0358	.0375
1.7	198.74	.2624	.4531	3.07	19.883	316.276	4.129	.00941	.00992
1.9	197.42	.2696	.5349	2.79	19.665	309.383	4.046	.00247	.0026
2.1	196.11	.2767	.6167	2.559	19.425	301.878	3.97	.00065	.000691
2.3	194.81	.2838	.6984	2.365	19.171	294.02	3.901	.000171	.000186
2.5	193.53	.2909	.7802	2.2	18.907	285.993	3.837	.0000448	.0000518

Table 1. The major parameters of a series of possible tokamaks with increasing major radius. All have a constant fusion gain of 5, aspect ratio of 1.8 and H_IPB98y2=1.9, and have reasonable density and beta limits, compressive stress and maximum field on the surface of the superconducting core. The radius of the core T_con increases slightly with major radius.

It is seen that the fusion power P_fus is roughly constant over the scan, as is the maximum stress. Another important parameter is the maximum field at the surface of the superconductor B_cond . This is seen to vary between 18.9 and 20.3 T, which corresponds to a feasible level for an HTS material at 30 K temperatures.

For all these runs the neutron and gamma fluxes were determined for the four angular bands, and as a function of energy, although with only 18 energy bands rather than the 60 used previously in this paper. The results from this series are given in detail in the supplimentary data associated with this paper. Figure 12 shows the total neutron and gamma fluxes crossing the mid-plane region of the outer surface of the superconducting core, integrated over energy, but including only fast particles defined as having energies greater than 0.1 MeV, and including all particle angles. It is seen that both neutrons and gammas approach a limiting exponential decay at plasma major radii above around 1 m. For neutrons, this limiting slope is 7.08 m^-1, as indicated by the short-dashed line in figure 12. For gammas, the limiting slope is rather higher as in the long-dashed line with the slope 7.38 m^-1.

Figure 12. The total neutron and gamma fluxes across the outside surface of the high temperature superconducting core as a function of the plasma major radius R₀ for the series of computations detailed in table 1. Only particles with energies >0.1 MeV have been included, following the definition of total flux used in reactor irradiation studies.

It is clear that at the lowest major radii below 1 m, when the shield thickness falls below 0.16 m, that both the neutron and gamma flux are appreciably lower than that expected from the exponential variation. At R_o=0.592 m where the shield thickness vanishes, the flux levels are fractions 0.283 and 0.258 of the expected exponential variation for neutrons and gammas respectively. This represents a favourable result since the fluxes are appreciably less than might have been expected from extrapolation of results at larger plasma radius. The differences can be well modelled by subtracting from the exponential variation the function: 5.45x10¹⁹exp[ - 14.56(E₀-0.592)] for the neutrons and 1.745 x10¹⁹exp[ - 16.25(R₀-0.6)] for the gammas. The solid lines in figure 12 show that a fit to within about 3% can be made to the whole flux variation with radius for both neutrons and gammas.

In figure 13 the total fast fluxes described in figure 12 are expressed as differential fluxes as a function of energy. The full lines and closed symbols represent neutron fluxes and the dashed lines and open symbols represent gammas. All fluxes refer to the outer surface of the HTS core, and for the mid-plane vertical section where fluxes are highest. The figure is important, as was figure 11, in that it describes the fluxes into the outer surface of the superconducting core that will determine how the superconductor lifetime may be estimated.

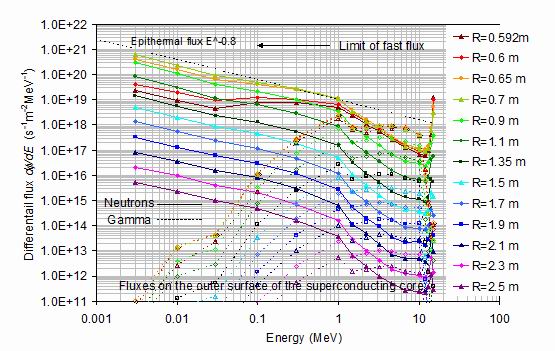
Generally, the neutron differential fluxes follow those shown in figure 7 that has a higher energy resolution. The rather sharp change of gradient of the neutron spectra at 1 MeV is clearly shown to be the upper edge of a broad fast neutron peak. This peak is most pronounced for major radii less than 0.65 m and then reduces rapidly at higher radii.

The gamma fluxes are appreciably higher than the neutron fluxes over the energy range 3 to 10 MeV. The difference is approximately a factor five and is maintained at all the plasma radii considered from R₀=0.6 to 2.5 m. At energies below 1 MeV they decrease quite rapidly with the differential flux dropping by 10³ for each decade of energy.

Figure 13. The total neutron and gamma fluxes on the outer surface of the superconducting core plotted as a function of energy for the various plasma major radii shown, following the parameters in the radial scan indicated in table 1. The neutron fluxes use full lines and closed symbols, the gamma fluxes use dashed lines and open symbols. An epithermal flux E^-0.8 is shown by the dashed line.

Figure 14. The total neutron and gamma fluxes at the outer surface of the superconducting core shown in figure 13, plotted as a function of major radius for given values of the energy, to make clear their variation with plasma radius at high energies. As before, the neutron fluxes use full lines and closed symbols, the gamma fluxes open symbols and dashed lines. 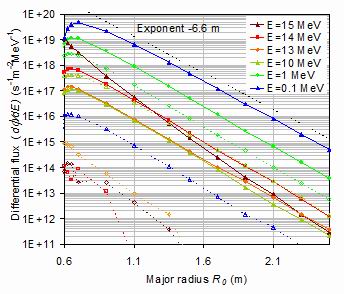The curves have a generally exponential dependence with a roughly constant exponent around -6.6 m^-1 similar to that shown in the total flux curves of figure 12.

Figure 14 shows the differential flux variations from 0.1 to 15 MeV in greater detail by expressing them as functions of major radius for selected energies. The curve defining the 14 to 15 MeV band includes the fusion 14.1 MeV neutrons and is seen to fall off relatively quickly with radius. However, even by the 14 MeV band the attenuation with radius is close to exponential and there is the same dip at low shield thickness that was seen in the energy-integrated flux. The magnitude of this dip increases as the energy decreases.

The gamma flux is naturally very low for 13 to 15 MeV energies but then rises rapidly and is some five times higher than the neutron flux at 10 MeV energies. By 1 MeV it is a similar factor lower and by 0.1 MeV a factor 104 lower. Thus, gamma radiation cannot be excluded but is quite limited in its energy range.

10. The expected lifetimes of High Temperature Superconductor tapes

In any fusion reactor, it is necessary that the HTS tapes withstand the radiation penetrating the shield for an acceptable time. Experimental studies to estimate this lifetime [6,10] have been performed by placing tapes in the central irradiation facility of the TRIGA Mark II fission reactor at the Vienna University of Technology [7]. The neutron dose was estimated by placing a nickel foil adjacent to the specimens and calculating the fast neutron fluence (E>0.1 MeV) from the activity of ⁵⁸Co, formed by the neutron capture reaction with ⁵⁸Ni. Experiments were performed up to an irradiation fluence of 3.9x10²² m^-2. The irradiations were carried out at the normal ambient reactor temperature.

After the various irradiations were complete, cryogenic tests of the superconducting properties were made. Results showed that the critical current when superconductivity was lost actually increased for low fluences of order 10²² m^-2 presumably as new magnetic flux pinning sites were created. However at larger doses the critical current and critical temperature decreased.

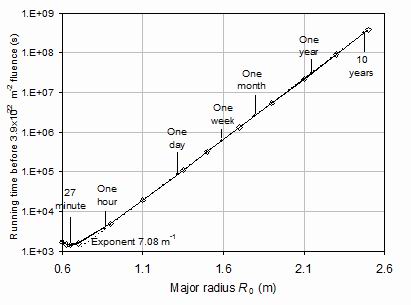
Figure 15. The expected cumulative running time, at full neutron production rate, before the fluence on the mid-plane of the HTS core reaches the value 3.9x10²² m^-2. This is the fluence where experimental data from fission reactor irradiation studies suggest the tape performance deteriorates significantly. The major radius is changed along with other parameters to allow fusion conditions as defined in Table 1.

The possible lifetime of the tapes may be estimated as a function of major radius for the series of nearly constant stress configurations given in Table 1, by estimating the neutron flux for energies >0.1 MeV as given in figure 12 and evaluating the number of seconds of continuous tokamak running time before the fluence reaches 3.9x10²² m^-2. Such a plot is given in figure 15. In practice the operating availability for such a first of a kind device would be very much less than 100% and as with fission; the best that can be expected is in the low 90's.

These results must be treated with caution because of several important differences between the fission reactor and tokamak HTS core irradiations. The fission reactor irradiation temperature was ambient rather than the 20 to 30 K at which the HTS is expected to run. This could mean that the damage creates new stable pinning centres, which could improve the superconducting properties, but there could be effects in the other direction; for example, the fluence at which the critical current begins to degrade could reduce. These effects may be annealed out during higher temperature irradiation. It is also important to note that the neutron and gamma fluxes from the fission reactor are likely to have different energy spectra from those behind the shield of the tokamak. The need is for irradiation facilities which could at least approximately reproduce the necessary flux distributions.

11. Conclusions

The flux levels and energy distributions of neutron and gamma irradiation on the high temperature superconductors of any fusion pilot plant are important because of the possible degradation of its superconducting properties at high fluence. Monte Carlo MCNP computations have been performed to compute the neutron and gamma fluxes within a 0.2 m radius high-temperature superconducting magnet shielded by a 0.32 m thick combination of layers of tungsten carbide and an optional tungsten boride layer separated by water cooling layers. The major radius for this part of the study was R₀=1.35 m and corresponded to the pilot plant suggested in [1]. The total neutron flux integrated over energy, and over all particle angles was shown to decrease exponentially through the shield with a half intensity distance of order 0.055 m. The gamma flux decreases at a similar rate. Within the superconducting core the neutron flux is roughly constant as shown in figure 4 with an averaged value of order 2.4x10¹⁷ s^-1m^-2. At this flux level a total neutron fluence of 3.9x10²² m^-2 would be achieved in 1.8 days.

The mean energy of the neutron flux was evaluated and shown to decrease much more slowly with a half intensity distance of 0.43 m. The mean energy of the gammas was seen to be almost constant over both shield and core with a value of order 2 MeV.

The neutron differential flux as a function of energy is rather flat in the epithermal region with an energy dependence of order 1/E^0.85. Above around 0.1 MeV it turns into a fast neutron distribution, which falls off steeply in the MeV range with a dependence of order 1/E^2.4. The gamma flux is comparable to that of the neutrons in the MeV range but falls off rapidly in the keV range.

The inclusion of the tungsten boride layer in the shield results in a strong attenuation of the neutrons in the eV range, although this corresponds to only some 20% decrease in the total energy-integrated flux. There is a corresponding increase in the gamma ray intensities.

The anisotropy of the fluxes was examined within four tallies of "into" and "out of" the core and at "wide angles" and "narrow angles". The anisotropy of 14.1 MeV fusion neutrons was shown to extend right through the shield and superconducting core. Gamma rays were shown to be preferentially generated in the tungsten part of the shield and to penetrate into the water layers.

The possibility of longer operating times was examined by performing a series of MCNP computations as a function of plasma major radius, designed to give a satisfactory and almost constant compressive stress in the core region. This scan, which allowed for an 8% increase in superconducting core radius as the major radius increased has been described by Sykes et al [9]. It showed that, given the same neutron fluence limit of 3.9x10²² m^-2, the lifetime of the device can be significanty increased from months to years by increasing the plasma major radius from 1.8m to 2.2m. This encouraging result helps validate the compact spherical tokamak route to fusion power and demonstrates that the neutron and gamma shielding required for reactor relevant operational lifetimes can be accommodated in a device of modest size.

Acknowledgements

The authors are grateful to Greg Brittles, Alan Costley, Robert Slade, George Smith and Alan Sykes for many fruitful technical discussions and cons`tructive criticism of the manuscript.

References

[1] Costley A. E., Hugill J. and Buxton P. F. 2015 On the Power and Size of Tokamak Fusion Pilot Plants and Reactors, Nuclear Fusion 55 033001
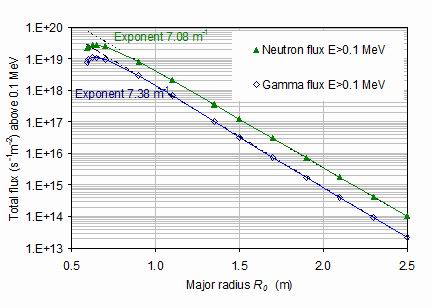
[2] Goorley T., James M., Booth T., Brown F., Bull J., Cox L. J., Durkee J., Elson J., Fensin M., Forster R. A., Hendricks J., Hughes H. G., Johns R., Kiedrowski B., Martz R., Mashnik S., McKinney G., Pelowitz D., Prael R., Sweezy J., Waters L., Wilcox T. and Zukaitis T. 2012 Initial MCNP6 release overview Nuclear Technology 180 No. 3 298-315
[3] Shultis J. K. and Faw R. E., 2011 An MCNP primer : http://bl831.als.lbl.gov/~mcfuser/publications/MCNP/MCNP_primer.pdf, , http://www.nucleonica.net/wiki/images/6/6b/MCNPprimer.pdf
[4] Windsor C. G., Morgan J. G. and Buxton P. F. 2015 Heat deposition into the superconducting central column of a spherical tokamak fusion plant published in Nuclear Fusion 55 023014
[5] Windsor C. G., Morgan J. G., Buxton P. F., Costley A. E, Smith G. D. W. and Sykes A. 2016 Modelling the power deposition into a spherical tokamak fusion power plant pubished in Nuclear Fusion 57 036001
[6] Prokopec R., Fischer D. X., Weber H. W. and Eisterer M. 2014 Suitability of coated conductors for fusion magnets in view of their radiation response Superconductor Science and Technology 28 0953-2048-28-01400528 https://doi.org/10.1088/0953-2048/28/1/014005
[7] Weber H. W., Bock H., Unfried E. and Greenwood L. R. 1986 Neutron dosimetry and damage calculations for the TRIGA MARK-II reactor in Vienna, Journal of Nuclear Materials 137 No 3 236-240 http://ati.tuwien.ac.at/reactor/EN/
[8] Temme, N. M. 2010, Voigt function, in Olver, F. W. J., Lozier, D. M., Boisvert, R. F., Clark, C. W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
[9] Sykes A., Costley A.E., Windsor C. G., Asunta O., Brittles G., Buxton P., Chuyanov V., Connor J. W., Gryaznevich M. P., Huang B, Hugill J., Kukushkin A., Kingham D., Morgan J. G., Noonan P., Ross J. S. H., Shevchenko V., Slade R, and Smith G., 2016 Compact Fusion Energy based on the Spherical Tokamak, Submitted to Nuclear Fusion , IAEA Fusion Conference (2016) Paper EX/P3 - 36.
[10] Chudy M., Fuger R., Eisterer M. and Weber H.W. 2011 http://ieeexplore.ieee.org/document/5721750/ Characterization of Commercial YBCO Coated Conductors After Neutron Irradiation IEEE Transactions on Applied Superconductivity 21 No. 3