First published in Physics Bulletin 39, 16-18, 1988

Biologists, physicists, computer scientists and engineers are united in believing that we now have a model for memory which is ready for use. How the model works can be understood by anyone and tested on any Microcomputer.

We can all see in ourselves some of the essential characteristics of human memory:

(i) memories need to be learnt and are built up by rehearsal;

(ii) we recall from a clue, or fragment of content;

(iii) memories decay gracefully with time, rather than catastrophically.

The puzzle of memory has not yet been solved, but many pieces in the jigsaw now fit together well. Progress is increasingly rapid as the picture begins to take shape: the references in the Further reading list tell the story. Here space only permits the description of one model, that proposed by Hopfield in 1982. It built on much earlier work, and has now been built upon in turn. However, his original model does show the characteristics of human memory mentioned above. It is not biologically realistic, but is straightforward and simple enough to program on a micro, so you can try it for yourself.

Neurons are the components from which our memories are built; one appears in figure 1, together with our representation of its essential constituents. In the classic model for their function, proposed back in 1943 by McCullough and Pitts. neurons are either on (black) or off (white). When on, the neuron fires and its output nerve, or axon, conveys a steady stream of action pulses to many other neurons (denoted by the hatching along the axon paths in the figures). It was realised by Hebb in 1949 that the key to memory lies in the host of interconnections, or synapses, which link the ends of the output axons of one set of neurons to the input nerves, or dendrites, of another set, so forming a complex network. The synapse strength varies chemically according to the tiring rate of both the incoming axon and the neuron. Although synapse strength, like axon firing rate actually varies smoothly over a range of values. in the model its strength is defined digitally - for example in the figures by the number of arrowheads. Each neuron is continually at work: it takes the products of the input signals from other neurons (1 or 0) with the corresponding synapse strengths (0. 1, 2 or 3 etc) and sums over all the connections. It switches itself on and begins firing if the sum exceeds some threshold (say 1.5. or half the maximum possible input) and switches itself off if the sum is below. All the neurons in the network are assumed to be continually updating their decisions in parallel, but unsynchronised with each other.

Positive and negative neurons (and synapses) occur, and indeed are an essential ingredient of this model: positive neurons and excitatory (round in figure 1) and negative ones inhibitory (oval). In one of nature's most elegant design rules, Na+ ions are transmitted through the selective ion channels in the synapses of excitatory neurons, and K+ ions through those in inhibitory neurons. An inhibitory neuron is switched off when the summed input is above a threshold, but switches on otherwise.

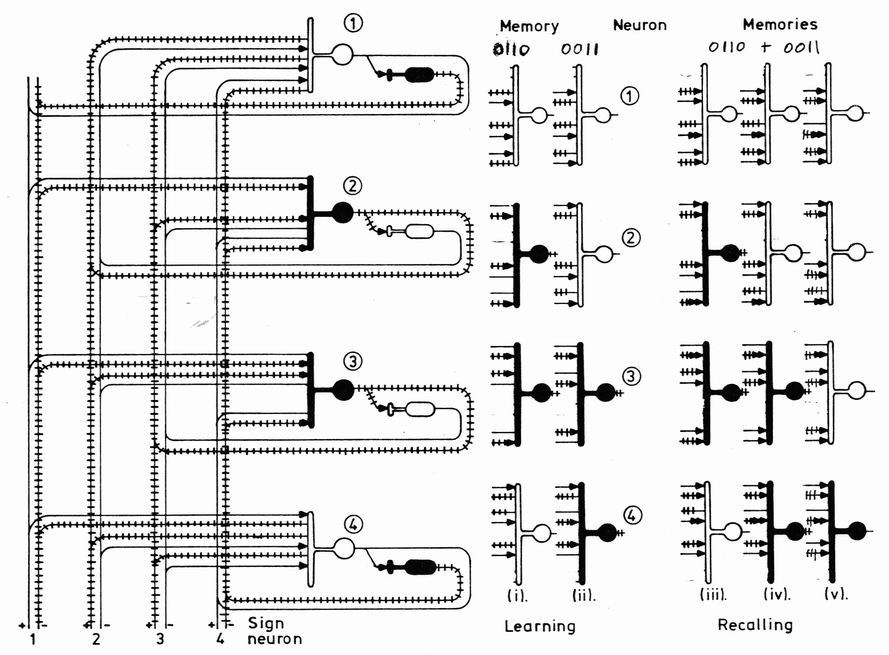
When we think of something - a picture, a note of music or a number - it is represented somewhere in our heads as a binary pattern of firing neurons. On the lefthand side of figure 2 the bus line at the bottom imposes the firing pattern 0110 on four excitatory neurons, one for each bit. Each pair of excitatory and inhibitory neurons connects with the dendrites of the other excitatory neurons, although not with its own. During meinorising, the synapse strengths are changed to make the desired firing pattern stable. Hopfield's recipe for the growth in synapse strength during learning is as follows:

(a) growth (one arrow) when a firing axon meets a firing neuron:

(b) no growth when a firing axon meets a nonfiring neuron;

(c) no growth when a nonfiring axon meets a firing neuron;

(d) growth (one arrow) when a nonfiring axon meets a nonfiring neuron.

The first three rules are easy to appreciate: passage of the action pulses through to a firing neuron increases the strength of the synapse. However, the last rule is not intuitive, and yet is essential to the success of Hopfield's model. The synapse grows in strength if both axon and neuron are non-firing. This symmetry between firing and non-firing neurons is responsible for the stability of the firing patterns, and also for one of the model's defects: it remembers black on white pictures in the same way as those with white on black. We are indeed equally at home with white chalk on a blackboard as we are with black ink on white paper. The arrows on the lefthand side of figure 2 are drawn according to these rules for the binary pattern 0110. The stability of the firing pattern in figure 2 can be tested by evaluating, for each excitatory neuron, the sum of the six products of axon activity and synapse strength, from the other neurons. Of the incoming axons to the dendrites of neuron I, the three firing axons all join at synapses of zero strength, so we have a thresholding sum of zero and the neuron stays off. The three firing axons approaching the firing neuron 2 all lead to arrowed synapses, so the sum reaches three and the neuron continues to fire. With only one pattern stored in the synapse strengths we would have a one-tracked mind. Any other neuron firing pattern would probably be changed into the stored pattern by applying the threshold rules a few times for each neuron.

Superimposing memories is simply a matter of coding the synapse strength changes for each pattern and adding them up. The righthand side of figure 2 indicates how this works out for the 0110 and 0011 patterns. Column (i). as on the left, defines the synapse strengths and neural actixities for 0110. whilst (ii) is the corresponding set for 0011. The other columns contain the memory of both patterns with synapse strengths equal to the sum of those from the first two patterns. The threshold must be increased as the mean signal rises. It is half the product of the number of superimposed pictures, and the number of neurons less one (a neuron does not send a signal to itself) or 2x(4 - 1)/2=3 in this example. Either firing pattern is stable under these synapse strengths. For example, the firing pattern 0110; neuron 1 has an input sum of 2 and so remains off, and the firing pattern is unchanged.

column (iii) has

This has a magic all its own. During recollection the synapse strengths remain at their values during memorising. A seed pattern (representing a hazy thought. An imperfect guess at a pattern) will, under a few thresholding procedures per neuron, approach the stable firing pattern it most closely resembles. Partial information will have recalled complete information, and this will have been retrieved through its content, not its location. Column (v) in figure 2 is an example of the seed firing pattern 0001. Neuron 3 has the thresholding sum of 4 and turns on to give our stable memorised pattern 0011. However, the choice of neuron must be taken randomly. Had we chosen neuron 1, the sum would have been 4, so the neuron would have switched on to give the pattern 1001 (the inverse of the other pattern). However, the stable state may not be one of the desired memories. If we try to remember too much - say if the ratio of stored pictures to neurons is larger than about 15% - then a random nonsense pattern may be obtained.

The act of recollection thus brings into play the very set of neuron firing patterns imposed during the learning process. The usefulness of revision exercises is obvious: if you want to remember something, recall it several times. Physicists will appreciate the helpful analogy of memories as minima in a multi-dimensional energy function, with the seed pattern rolling down into the nearest local minimum. The theory of spin glasses can assist in understanding the process.

With a BASIC language program on a home computer (see box). you should be able to converge 5X5 pictures (25 neurons) in a few minutes. My family loves animals, and so memorised pictures of a man, a dog and a horse are given in the lower half of figure 3. The upper figures illustrate seed patterns, the arrows indicating the memories to which they will converge. Picture (iv) is the man but with 30% of its pixels or elements randomly changed in sign. It is only just recognisable. but successfully finds the correct memory. (v) is the barest minimum expression of a dog (just its nose), but again it is sufficient to recover the full image. Graceful degradation is illustrated in (vi), where the horse of (iii) has been entered as the seed but 30% of the synapses have been randomly altered to one of their allowed values of 0. 1. 2 or 3. It is still recognisable despite this treatment, vhich would leave man's computer memories in chaos.

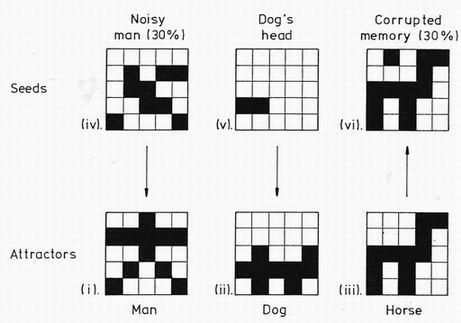Figure 3 Some examples of the performance of a 25-neuron pair network, with synapse strengths calculated from the superposition of those for the attractor pictures (i), (ii) and (iii). Seed (iv) shows the man with 30% of the pixels changed in sign; it successfully follows the arrow to the correct attractor. (v) has just a fragment of the dog (his nose); again it is sufficient to find the correct attractor. (vi) shows the effect of corrupting 30% of the synapse strengths to random values. Using the horse (iii) as a seed gives the new attractor (vi), almost unchanged from the original.

The method of memory recall is often best employed in thc very situations in which humans have not proved easy to replace. Reading our distinctive handwriting and typing out our speech are subjects of much current study. Recognising ultrasonic images in the presence of both random noise and striped background is one aspect we are working on here. The method can be taught to ignore some images. as well as selecting others. Our universal love of rhythmic music, if nothing else, tells us that our firing patterns are not stable states but cycles of recurring patterns. This feature does arise from the model if the synapse strengths are assumed to be asymmetric. It is easy to modify the learning procedure so that a sequence of cyclic patterns is stored; they are then recalled by a cyclic set of seed patterns. This is just the process required for identifying the tell-tale sound of a failing bearing in a noisy engine. These applications require rather more detailed procedures than have been described here, as well as much larger arrays of neural elements. We have a long way to go before we can approach our brains with their 10 billion neurons and 10 thousand billion synapses! The fact that we cannot yet attain the brain's performance should not deter us from using its ideas.

I should like to express my thanks to Andrew Chadwick, Alan Penn and David Wallace for their inspiration and advice on the manuscript.

Hebb D O 1949 The Organisation of Behaviour (New York: John Wiley)

Kohonen T 1977 Associative Memory: A System Theoretical Approach (New York: Springer)

Hopfield J J 1982 Proc Natl. Acad. Sci. (USA) 79 2254

Rumelhart D E and MeClelland J L (eds) Parallel Distributed Processing (2 vols) (Cambridge: MIT Press)

The original BASIC version for the BBC, Sinclair Spectrum and MSBASIC languages.

A more modern Microsoft QuickBasic version.