
Unpublished paper: prepared for Proc. Phys. Soc in 1963
C. G.
Windsor*, Clarendon Laboratory, Oxford, England
*Present
address: A.E.R.E., Harwell, Berks., England
Paramagnetic
resonance experiments are described on exchange of coupled pairs of Mn++
ions present in the KMgF3 lattice. The nearest neighbour (nn)
exchange interaction JSi.Sj
is found to be dominant, with the value Jnn =
+4.5 ± 2 oK. The interaction between next nearest neighbours
(nnn) is found to be so small that pair transitions between states of different
total spin, which are normally forbidden, become weakly allowed. From the
positions of these transitions the exchange interaction Jnnn = +0.043 ± 0.005 °K is determined.
Paramagnetic
resonance experiments on exchange coupled pairs of ions in a dilute magnetic
lattice provide a direct means of determining exchange interactions between
given
neighbours
in the lattice. Previous Mn++
pair experiments have been performed on the MgO lattice by Coles et
al 1960) and Harris and Owen (1963) and on the ZnF2 lattice by
Brown et al (1961). We now describe Mn++ pair experiments on
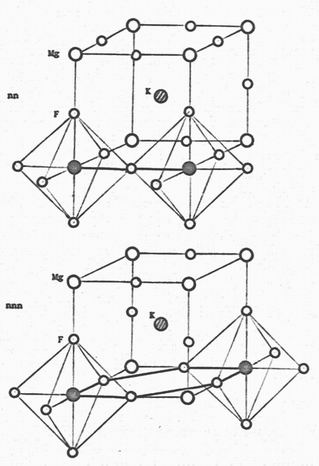
the KMgF3 lattice. Figure 1 shows the structures of nearest neighbour
(nn) and next nearest neighbour (nnn) pairs in this perovskite structure. Salts
of this structure are particularly suitable for theoretical studies. The
magnetic ions lie on a simple cubic lattice although this may distort at low
temperatures. Also, as the present results confirm, the magnetic properties are
dominated by one type of interaction.


Figure 1:
The
structure of nearest neighbour and next- nearest neighbour pairs in the
KMgF3
lattice.
We
describe our results by a Hamiltonian with axial symmetry along a bond
axis
where
Si =
Sj =
5/2; De contains a dipolar term (
-g2b2/rij3)
together with possible anisotropic exchange. Hi,Hj
are the Hamiltonians of the isolated ions, each of form
Hi = g bH.Si
+ Dc
{(Szi) 2 - 1/3 Si.(Si
+ 1) } +
FcO40(Si)/180
Here
O40(Si) represents the usual fourth order
crystal field operator (Bleaney and Stevens, 1953). This Hamiltonian may be
written in a form diagonal in the isotropic exchange by expressing in terms of
the total spin S = Si + Sj. The Hamiltonian (1) then
becomes
H = Ss Hs
(2)
for
S = 0, 1, 2 ... (Si +
Sj
), where
Hs = g bH.S + ½J{ S(S + 1)
- Si.(Si + 1) - Sj.(Sj + 1)
}
+(3as
De
+
bs Dc )
{Sz2 - 1/3S(S + 1)
} +
gs
FcO40(S)/180
(3)
Expressions
for the numerical constants as
, bs are
given by Owen (1961). The expression for gs
is derived by Windsor (1963):
gs =
[
35S2(S +
1)2 -
180 S(S
+ 1) +
180 - 120 S(S +
1)Si(Si + 1)
+ 48
(Si)2(Si + 1)2 +444 (Si)(Si
+ 1)
]/
4(25+3)((25+5)(25-3)(25-1)
(4)
In
previous Mn++ pair experiments, and in the nn pairs reported here,
this Hamiltonian is dominated by the isotropic exchange. The dipolar and crystal
field terms are non-diagonal in this representation but the admixtures between
states of different total spin will be of order D/J, and therefore small in this
case. The allowed transitions are given by the selection
rule
DS
= 0
DSz
= ±1
(5)
so
that these transitions may be found by solving the sub-Hamiltonians (3) for each
value of the total spin. This is a very much simpler problem than solving the
original Hamiltonian (1) but gives results in error by amounts of order
D2/J. The positions of these transitions do not depend on the value
of the isotropic exchange, which must therefore be deduced from intensity
variations.
When the condition that isotropic exchange is dominant in the Hamiltonian
is relaxed, the matrix elements of the dipolar and crystal field terms between
states of different total spin induce extra "forbidden" transitions. In the
extreme case when all the terms are comparable, the analysis is formidable. Such
a case has been studied by Hutchings (1964) for Gd+++ pairs in
LaCl3.
However in the
intermediate case when the exchange interaction is just a few times larger than
the other terms the observed spectrum is still fairly simple to analyse and
offers the prospect of measuring the exchange interaction from line positions
alone. Thus the dipolar interaction has matrix elements connecting states for
which DS = ± 2 DSz = ±
0 . The resultant admixture of states gives rise to forbidden transitions whose
intensity is of order (De/J)2 of the allowed transitions, and which
obey the selection rule
DS = ± 2 DSz =
± 1
(6)
If the exchange is still
relatively large, these transitions give rise to nearly isotropic groups of
lines on each side of the main line. These groups are then split by the other
terms in the Hamiltonian. The line positions can be found to first order in
De/J and Dc/J from Hamiltonian (3). With the external
field parallel to the pair axis, we find the positions of the transitions where
S<-> (S-2), S <= ZSi, and where ±SZ <-> ±(Sz
- 1), SZ<=S,
are given by
gbH
= hn m (2S-1)J + As,sz
De
+
Bs,sz Dc
where
As,sz
=
[-18(Sz
- S)2 + (6Sz -4S - 1)(2S - 1)(S - 3)(S + 2) –
12Si
(Si + 1)(4Sz - 2S - 1)(2Sz - 1)]/
2(2S+3) (2S-1)
(2S-5)
and
where
Bs,sz = -2/3 As,sz
+ 1/3 (6Sz - 4S - 1)
(7)
This
is the situation we report here for nnn Mn++ pairs in
KMgF3. The isotropic exchange is some four times bigger than the
dipolar interaction, other terms being negligible. The forbidden lines thus have
intensity of order 1/16 of the ordinary pair lines, and are definitely
observable.
Lastly
we consider the effect on the pair spectrum of other possible terms in the
exchange Hamiltonian. An anti-symmetric exchange term D.
Si x Sj has been shown by Moriya (1960) to
arise on the super-exchange model when orbital admixtures are included, and may
lead to canting of spins. It is found that the term has no matrix elements
between pair states of the same total spin and so has no first order effect on
the pair spectrum when the isotropic exchange is dominant. If the term were
appreciable compared to the isotropic exchange then second order shifts of order
ïDï2/J
and forbidden transitions where DS
= ±1 may be observed. Moriya (1960) has shown that if the centre of the pair is
also a centre of inversion then anti-symmetric exchange must vanish. This
condition applies to both nn and nnn pairs in KMnF3, showing that the
canting in this material must be from some other cause.
Biquadratic exchange -j(SiSj)2 has been
shown by Harris and Owen (1963) to be of importance in MnO. The term is
isotropic and so does not effect the positions of allowed transitions. Their
intensities are modified however and this is discussed
later.
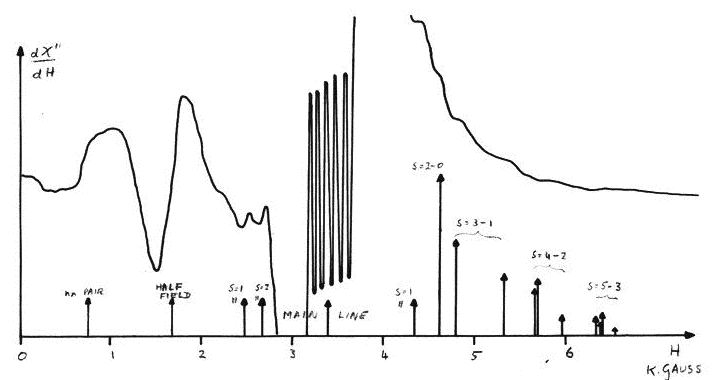

Figure
2 The paramagnetic resonance absorption (differentiated) from a KMgF3
crystal containing nominally 5% of Mn++, as the magnetic field is
swept in a (100) direction. The
microwave frequency was 9500 Mcs (X-Band), and the temperature 20°K. The spectrum shows transitions from
nearest neighbour pairs both parallel and perpendicular to the field
direction. The arrows show the
calculated line positions for the parameters of table
1.
Figure
2 shows the experimental spectrum observed along a (100) direction where
transitions from nn pairs with axes both parallel and perpendicular to the
external field are seen. The figure shows clearly the large linewidth of order
400 Gauss, caused by unresolved manganese and fluorine hyperfine structure which
has severely limited the accuracy of both line position and intensity
measurements. The anisotropy constants of table 1 were found by fitting the
positions of some fifteen transitions, measured both at X and Q band
frequencies, and at several temperatures, to the Hamiltonian (3). Figure 2 also
shows the theoretical line positions calculated according to these parameters.
The sigma of the nn anistropy constants were found from the temperature
variation of the intensities (Windsor, 1963). Table 1 also shows the calculated
dipolar interactions for the host and concentrated lattices. It is seen that the
observed interaction is consistent with mainly dipolar
anisotropy.
Table
1. Spin Hamiltonian Parameters for Mn++ Pairs in
KMgF3
|
|
Nearest
neighbour |
Next-nearest
neighbour |
|
J
oK |
4.5
± 2 |
+0.043
± 0.005 |
|
Dc
cm-1 x
10-4 |
120
± 30 |
+3.3
± 5 |
|
Fc
cm-1 x
10-4 |
63
± 30 |
- |
|
De cm-1
x 10-4 |
171
± 50 |
-76
± 5 |
|
-g2b2/rij3 cm-1 x 10-4
(host |
-270
|
-96
|
|
(conc |
-235
|
-83 |
|
|
|
|

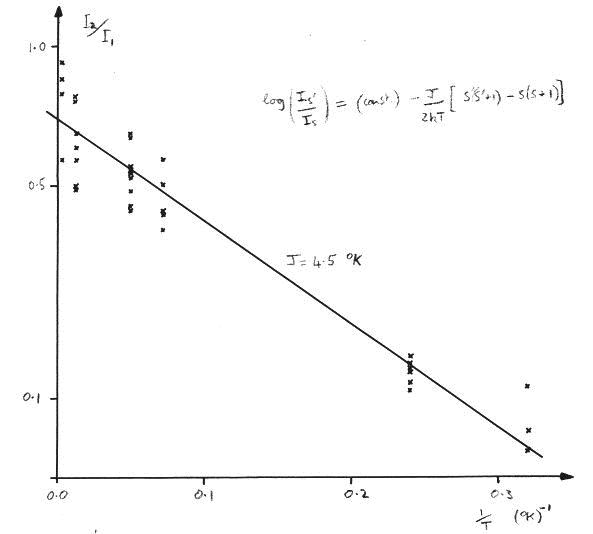
Figure 3: The logarithm of
the intensity ratio of pair transitions with S=2 and with S=1 plotted against
inverse temperature. The
measurements apply to the two lowest field lines observed with the external
field in a (100) direction, and at 36,000 Mcs frequency (Q
band).
The
isotropic exchange was deduced from a comparison of the intensities of
transactions between states of different total spin. The value given in the table was deduced
from measurements at Q band frequencies of the intensity ratio of lines from S=2
and S=1 states over the temperature range 300 - 2.2 oK. These
measurements are plotted in figure 3.
The intensities of transactions from higher spin states were consistent
with this value, but not sufficiently accurate to determine any biquadratic term
j(SiSj)2
in the exchange Hamiltonian.
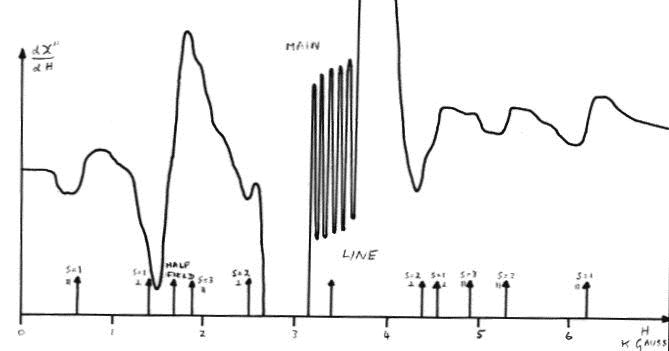
 Figure 4: The spectrum along the (110)
axis of next nearest
neighbour
pairs recorded under the same conditions as in figure 2. The intense lines at low fields are from
allowed transitions. The weaker
lines seen at high fields are ascribed to nnn forbidden transitions. The arrows show the calculated positions
and relative intensities of these lines for the parameters of table
1.
Figure 4: The spectrum along the (110)
axis of next nearest
neighbour
pairs recorded under the same conditions as in figure 2. The intense lines at low fields are from
allowed transitions. The weaker
lines seen at high fields are ascribed to nnn forbidden transitions. The arrows show the calculated positions
and relative intensities of these lines for the parameters of table
1.
Figure 4 shows the
experimental spectrum observed along the (110) axis of nnn pairs. The two intense transitions seen just
below the main line show just the anisotropy expected from the two outer
transitions of nnn pairs. Fitting
the positions of these two lines to Hamiltonian (3) gives the values of
De and Dc shown in table 1. The figure also shows several weaker
lines seen best at high fields, whose splittings from the main line are too
large for them to be ascribed to either nn or nnn allowed transitions. From the intensities and anisotropy of
these lines we ascribe them to forbidden transitions of the type described
earlier. The exchange interaction
was adjusted to give the best fit with the spectrum taking the values of De and
Dc found above. Figure 3 also shows
the positions and relative intensities of the forbidden transitions calculated
with the parameters of table 1. The
two outer groups of lines are not resolved in the figure, but an examination
with better resolution shows these to be groups of lines as predicted. It is seen that there is completely
satisfactory agreement within the errors of order 50 Gauss caused by our neglect
of second order terms in calculating the line positions.
We
regard the main result of this work as the verification that only nearest
neighbour interactions are of importance in this perovskite structure. It would
be interesting if the experimental ratio Jnnn/Jnn= 0.010 ±
0.004 could be derived from theoretical considerations.
In
the light of the above conclusion it is likely that the Bethe-Peierls-Weiss
calculation of the nn exchange interaction from the Néel temperature will be
particularly accurate, since this method relies on a one interaction
supposition. Table 2 shows the value calculated by Smart (1963) using this
method compared with determinations by other methods.
Table
2. The Nearest Neighbour Exchange Interaction in
KMnF3
Method
|
From
TN (BPW) |
From
X(TN) |
From
q
|
From
paramagnetic neutron scattering |
From
pairs in KMnF3 |
Jnn
oK |
6.2 |
7.2 |
9.0 |
6.2 |
4.8
±2 |
|
Reference |
Smart
(1963) |
Smart
(1963) |
Hirakawa
et al (1960) |
Collins
and Nathans (1964) |
Present
work |
The
pair result seems distinctly low compared with the other values, especially
since the increase in lattice constant from 4.00A in KMgF3 to 4.198
in KMnF3 would suggest a still lower value for comparison with
results on the concentrated salt.
It
is possible that the discrepancies may be resolved by including a biquadratic
exchange term -j(SiSj)2 in the pair
Hamiltonian. The pair experiment measures the quantity J(1 + 13.5j/J) and is
thus modified by quite small values of j/J. Preliminary calculations by Windsor
(to be published) suggest that the value of exchange deduced from the
Curie-Weiss ( q )
is given by J(1 - 0.5 j/J) while
the values deduced from the Néel temperature and from paramagnetic neutron
scattering are not appreciably changed. The discrepancies between
the various results are then resolved by assuming j/J = -0.025 ±0.01
with J =6.5±1
°K.
This
ratio of j/J is less in magnitude than that found by Harris and Owen (1963) for
Mn++ pairs in MgO, although the change in sign is
unexpected.
`The
authors are very grateful to Drs. Owen, Griffiths and Harris for help and
encouragement in this work.
B.
Bleaney and K.W. H. Stevens, Rep. Prog. Phys.,16, 107, 1953.
M.R.
Brown, B.A. Coles and J. Owen, Phys. Rev. Lett. 7, 246, 1960.
B.
A. Coles, J. W. Orton, J. Owen, Phys. Rev. Lett. 4, 116,
I960.
M.
F. Collins, H. Nathans, J. Applied Physics (To be published).
E.A.
Harris, J. Owen, Phys. Rev. Lett., 11, 9, 1963.
K.
Hirakawa, K. Hirakawa, T. Hashimoto, J. Phys. Soc. Japan, 15, 2063,
1960.
M.
Hutchings, Proc. Nottingham Conference 1964, (To be published).
T.
Moriya, Phys. Rev. 120, 91, 1960.
J.
Owen, J. App. Phys. 32, 2135, 1961.
J.
S. Smart, Magnetism, edited by Rado & Suhl, Academic Press, 1963, Page
90.
C.
G. Windsor, Thesis, Oxford 1963. (Unpublished).