Neutron-scattering data for paramagnetic nickel have recently become available,^1,2 surveying the magnetic cross section as a function of energy transfer hw/2p and momentum transfer hK/2p up to about 1/8 eV throughout the first Brillouin zone in just sufficient detail to allow comparisons to be made with theory.^3,4 Recently, Lowde and Windsor ^5,6 gave an analysis of the results at 1.67T_c in terms of free-electron gas theory and found that an absolute fit could be obtained if a random-phase approximation (RPA) enhancement of 3 +/- 1 were applied to the theoretical susceptibility, the parameters of the best-fitting gas then being in good agreement with what is estimated from other arguments. Comparison with a free gas, however, could be made only for K's up to about 1/2K_max, since the periodicity of the crystal gives rise to umklapp processes which have a pronounced effect on the scattering at larger K's but which are not allowed for in the free-gas calculation.

Clearly it would be desirable to compare these data with high-quality calculations representing the various theoretical treatments of magnetism in metals. As an intermediate step we have per formed a simple tight-binding computation of the generalized susceptibility. Such an elementary expedient lacks a number of the refinements that could, technically, be incorporated with a greater effort; but it does make proper allowance for crystal periodicity and for the band multiplicity, and it calls for comparison with the whole set of data. In fact, a surprisingly good fit to the data is obtained, with approximately the same RPA enhancement factor as derived before.

We first computed the imaginary part

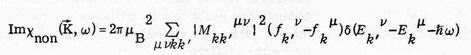(1)

of the Lindhard susceptibility expression, the f's being temperature-dependent Fermi-Dirac occupation factors and the sum running over the Brillouin zone of electron wave vectors k,k' and all five values of each band index m, n. The real part was then derived from (1) using the Kramers-Kronig relation, the integral in that relation being extended over the complete range for which Imc is nonzero.

In the approximation of extremely tight binding, where overlap of neighboring atomic wave functions is ignored, the matrix element M_kk'^nm can be written

(2)

where G is an umklapp vector and the c's are the coefficients of the 3d orbitals (p in the one-electron wave functions

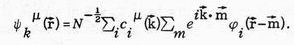(3)

We assumed that the integral in (2) may be approximated by the atomic form factor F(K); thereupon its independence of i and j allowed us to write

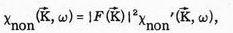(4)

with c' the reduced susceptibility of Izuyama, Kim, and Kubo,⁷ and to concentrate attention on calculating c' from the c's and E's.

The coefficients c_i^m(k) and the one-electron energies E_k^m were determined using the procedure given by Fletcher,⁸ employing the integrals (over the Hartree-and-Hartree 1936 wave functions for Cu⁺ of his Eq, (18) after multiplication with the factor p/2 by which they were in error.⁹ The Fermi surface and density of states obtained for nickel in, this way have recently been re-examined by Allan¹⁰ and found to reproduce, albeit roughly, many of the features of the more sophisticated theories; for instance, the density of states at the paramagnetic Fermi surface at absolute zero comes to 2.5 eV^-1atom^-1 (spin state)^-1 as against a preferred 2.1, and the total d-band width is 4.2 eV as against a preferred 4.5. Summation over the Brillouin zone in (1) was performed for the 356 points of a mesh of spacing k_max/14 that fall into the fundamental 1/48, and an energy histogram was constructed to a base unit of 0.02 eV showing the susceptibility as a function of hw/2p.

Figure 1 shows both real and imaginary parts of the unenhanced, reduced, tight-binding susceptibility at 1020 ⁰K for three of the 14 selected values of K along the <100> direction. Where the comparison with a free-electron gas is meaningful, i.e., the central part of the zone, the results are very strikingly similar to those for a free gas. The limiting lines of our c' at small K and w are those-of a free gas of K_eff= 1.3 +/- 0.1 Ǻ ^-1 and E_F= 0.37 +/- 0.03 eV, which are almost exactly the free-gas values giving the best fit of Lowde and Windsor to the experimental data.

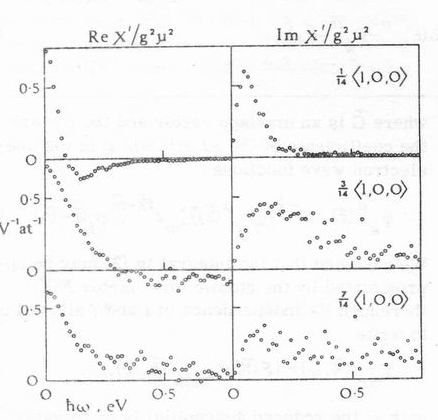
FIG. 1. The reduced susceptibility c_non'(K,w)at 1020 ⁰K for a metal having no exchange enhancement and the constants of paramagnetic nickel as calculated to tight-binding approximation for the five 3d bands only.

It may be assumed that the true c' is a smooth function on a scale of detail of the order 0.05 eV, and that the small-scale irregularities in Fig. 1 are caused by the coarseness of our mesh in reciprocal space. In the first place, at any given K the factor f_k'ⁿ- f_k^m averages the matrix element very extensively over the occupied volume of the zone, thus diminishing the influence of any local peculiarities in E(K. Moreover,³ the susceptibility of a metal at an elevated temperature is effectively a weighted mean of the susceptibilities c_E at 0 ⁰K of models having the bands filled to an energy E:

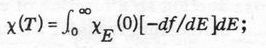(5)

Our expectation that the theoretical structure of the high-temperature susceptibility is such as to minimize its dependence on fine detail in E(k) is borne out by the fact that the neutron-scattering data show a gently varying function and that no anisotropy was observed within the error of measurement. Indeed, since anisotropy was not detected, we have regarded it as sufficient in the first instance to calculate c' for the one direction of K only (the <100> direction), and for comparison purposes we collapse all the experimental data on to a single parameter |K| to improve the statistics.

The power spectrum S(K,w) of the spin fluctuations in paramagnetic nickel, derived from the neutron-scattering cross section via

(6)

[in conventional notation, where again we extract |F(K)|² from S in the interests of simplicity], is related to the reduced susceptibility by

(7)

FIG. 2. An absolute comparison between the power spectrum S(K,w) of spin fluctuations in nickel at 1020°K as observed by neutron scattering and as calculated from the tight-binding model of Fig. 1. Dotted lines denote no enhancement of the susceptibility; solid lines denote the assumption of an effective Coulomb interaction I_eff(k)=0.52 eV; dashed lines denote the effect of using I_eff(k)=0.32 eV. .

Our theoretical unenhanced S is illustrated by the dotted line in Fig. 2 and is seen to be in severe disagreement with the data. However, according to Izuyama, Kim, and Kubo ⁷ the effect in RPA of a Coulomb repulsion term in the Hamiltonian is to enhance c' as it were by a molecular field, and it is not difficult to show that with the most general RPA the molecular-field constant is the Fourier transform I_eff(k) of the effective Coulomb repulsion integral I_eff(r). Then

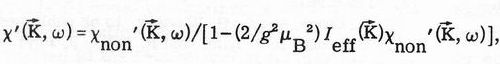(8)

and hence⁴

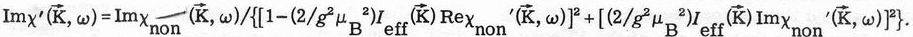(9)

Using I_eff(k)=0.52 eV, independent of K, a considerably more realistic function is obtained as demonstrated by the solid lines in Fig. 2. Bearing in mind that the calculation is absolute except for the adjustment of a constant I_eff(k) the general tendency of the solid lines to follow the data throughout the zone is remarkable.

Further study of the situation shows that the best-fitting solid lines in all cases fall below the data at the larger energies. The more obvious weaknesses of our calculation would not be capable of producing this effect, and so if it is not just a defect of the data, the question arises whether it has a deeper significance. We wondered, in fact, whether it might not be wrong to explain the extra susceptibility observed over and above the unenhanced d-spin contribution simply by invoking an enhancement factor. Conceivably the explanation might be that there are other contributions to the susceptibility from s electrons and from the orbital moment, for instance. By way of an attempt to explore this possibility, without having a quantitative estimate to support it, we have tried the effect of arbitrarily doubling the 3dc_non' and employing a lesser enhancement factor than before. The use of a constant I_eff(k)=0.32 eV then produces the markedly improved fit exhibited by the broken lines.

Both the calculations with enhancement shown in Fig. 2 give a notable degree of fit with a constant I_eff(k)=0.52 eV. In the latter case (with the arbitrary factor of 2) the function derived is realistic enough to allow fitting to be performed at the different K's individually. The resulting I_eff(k)=0.52 eV is shown in Fig. 3, and within the uncertainty of the work is constant at 0.33 +/- 0.03 eV.

FIG. 3. I_eff(k) the Fourier transform of the effective Coulomb interaction I_eff(r) for nickel at 1.67T_c.

A corresponding set of fits with the completely absolute calculation corresponding to the solid lines in Fig. 2 can be made only if the data for hw/2p 0.05eV are ignored on the assumption that the discrepancy at higher energies may be disregarded for some unknown reason. We cannot justify abandoning the higher energy measurements, but it is reassuring to note that if the absolute calculation be fitted where it can be, below 0.05 eV, an equally nearly constant I_eff(k) is obtained of mean value 0.52 +/- 0.04 eV. The reason is that the K dependence of the enhancement is much more pronounced at low energies; the two fits, taken together, suggest that the observed virtual independence of K is a feature of the work not particularly sensitive to the detailed explanation assumed.

I_eff(k) be taken at its face value, accepting uncritically for the moment that an estimate of S from an unhybridized tight-binding model can be relied upon to this degree, it would follow that the Fourier transform I_eff(r) is close to a delta function in form. This is in accordance with the long-familiar view that intra-atomic Coulomb repulsion is the dominant factor determining ferromagnetism in nickel. Assuming there is no contribution from the atoms beyond the nearest-neighbor positions, Fig. 3 would suggest that any one of the 12 nearest neighbors to a nickel atom contributes less than 10% of the on-site term at r=0 to the "effective Coulomb integral" if the contribution is of the same sign, and less than 5% if the contribution is of the opposite sign. Both these limits are materially lower than the ~30% contribution estimated by Clogston¹¹ for nearest neighbors in palladium.

The latter value 0.52 +/- 0.04 eV for I_eff corresponds to a susceptibility-enhancement factor at 1020K of 5.5 _+/- 1.5, which may be compared directly with the factor 8 obtained on dividing the measured ¹² susceptibility at 1020°K by an estimate of the integral of 0.5g²m_BN(E)[-df/dE]dE from the best available density-of-states curves.¹³

¹ J. W. Cable, R. D. Lowde, C. G. Windsor, and A. D. B. Woods, J. Appl. Phys. 38, 1247 (1967).

² D. Lowde and C. G. Windsor, to be published.

³S. Doniach, Proc. Phys. Soc. (London) 91, 86 (1967).

⁴S. Doniach, in Rendiconti della Scuola Internazionale di Fisica "Enrico Fermi," XXXVII Corso, edited by W. Marshall (Academic Press, Inc., New York, 1967), p. 319.

⁵D. Lowde and C. G. Windsor, Phys. Rev. Letters 18, 1136 (1967).

⁶R. D. Lowde and C. G. Windsor, to be published. (see: R. D. Lowde and C. G. Windsor, On the Magnetic Excitations in Nickel. Adv. Phys. 19, 813-909, 1970.)

⁷T. Izuyama, D. J. Kim, and R. Kubo, J. Phys. Soc. Japan 18, 1025 (1963).

⁸ C. Fletcher, Proc. Phys. Soc. (London) 65, 192 (1952).

⁹J. L. Beeby, private communication.

¹⁰G. Allan, thesis, Faculte des Sciences d'Orsay, 1967 (unpublished).

¹¹A. M. Clogston, Phys. Rev. Letters 19, 583 (1967).

¹²S. Arajs and R. V. Colvin, J. Phys. Chem. Solids 24, 1233 (1963).