
PROC. PHYS. SOC., 1967, VOL. 91. PRINTED IN GREAT BRITAIN
Spin correlations in a classical Heisenberg paramagnet
C. G. WINDSOR
Solid State Physics Division, Atomic Energy Research Establishment, Harwell, Didcot, Berks.
MS. received 7th February 1967
Abstract. A computer model of a Heisenberg paramagnet is constructed from a thousand classical spin vectors situated on a simple cubic lattice and interacting through nearest-neighbour exchange forces. The motion of an initial random set of spins is calculated explicitly and used to evaluate the correlations <
S0(0).SR(t)>
as a function of time for various neighbours. The neutron scattering from a poly-crystalline paramagnet is predicted from the correlations and compared with experimental data on RbMnF3.
The spin correlations in a Heisenberg paramagnet have been calculated by solving numerically the motion of the spin vectors on a finite lattice of classical spins. A simple cubic array of a thousand spins was set up with some initial set of spin directions. The equation of motion of any individual spin SR is determined by its commutator with the Hamiltonian. If we assume Heisenberg exchange interactions 2J Si.Sj, between nearest-neighbour spins this may be evaluated to give
dSR/dt = 2pi/h [H , SR ] = - 2J 2p/h SR' nn R SR.SR'
The spin changes DSR in a short finite time Dt were evaluated for every spin in the lattice at successive times updating all the spin directions at the end of each time interval. Periodic boundary conditions were used so that all spins in the lattice were equivalent. At infinite temperatures any random set of spin directions sufficed as a possible initial spin configuration. At finite temperatures, not considered here, a configuration must be found where the initial energies of the spins satisfy a Boltzmann distribution (Harris 1964). If the time increment Dt is small compared with the natural unit of time h/2JS/2p, the motion of the whole spin system is determined as a function of time. It is then straightforward to evaluate the correlations <S0(0).SR(t)> between an initial spin direction and that of a neighbouring spin distant R observed at a later time t. In this classical approximation the expectation value could be interpreted as a simple average taken over all equivalent neighbours in the finite lattice and possibly also over different initial spin configurations. Figure 1 shows the correlations calculated for spins on the same site and on the first-, second- and third-neighbour positions of a simple cubic lattice. The curves have a statistical error of order 0.01Ö
zR depending on the multiplicity ZR of each type of neighbour, but are substantially independent of the size of the lattice, the initial spin configuration and the finite size of the time increment used in calculating the motion. Conservation of total spin requires that the sum of the correlations over all neighbours should be constant independent of time (de Gennes 1958). The curve labeled 24 in figure 1 shows this sum for the correlations recorded in the computation. Its deviation from unity represents the contribution of correlations from more distant neighbours. These become rapidly more difficult to compute as their magnitude approaches the statistical error. For sufficiently remote neighbours the classical theory of diffusion through a uniform medium should apply. In fact, the correlations calculated using this theory (de Gennes 1958) are in only qualitative agreement with the computed curves. The correlations are observed to be even functions of time. It follows that the correlations in a ferromagnet and in an antiferromagnet are identical in this infinite temperature limit.
A double Fourier transform of the correlations over space and time gives the function. S(K, w), closely related to the neutron scattering observed with momentum transfer hK/2p, and energy transfer hw/2p:
S(K, w) = SR eiK.R/2p ò
-¥
¥
e-iwt <
S0(0).SR(t)>
dt.
Direct Fourier transformation of the computed correlations has been attempted but poor resolution in K and w results from the lack of data with R > 2 and t > 4h/2JS/2p. A more
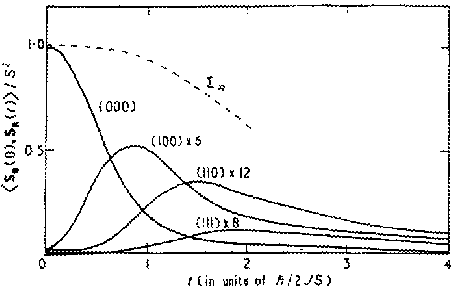
Figure 1. Spin correlations between various neighbours in a simple cubic paramagnet with nearest-neighbour Heisenberg exchange interactions. The correlations are multiplied by the multiplicity of each type of neighbour. The lattice contained 1000 spins and the results were averaged over 10 different initial configurations. The time increment used in calculating the motion was 0.01 units. The data required over two hours computing time on an IBM 7030.
accurate estimate may be made of the scattering from a polycrystal where the average over directions of K replaces the exponential involving K in the above equation by (sin KR)/KR. As was pointed out by de Gennes (1958), when K > p/R this factor becomes small, except when R = 0, causing the scattering to become nearly independent of K and to depend mainly on the transform of the same-site correlation <
S0(0).S0(t)>
and this is shown by the smooth curve in figure 2. Little difference results if the correlations for t > 4h/2JS2p are simply truncated or if they are extrapolated at large times according to the t-3/2 law

Figure 2. Neutron scattering from a polycrystalline paramagnet. The curve is the Fourier transform of the same site correlation. The points are data from RbMnF3 at 300 0K (T/TN = 3 7), at 200 scattering angle and using 3.0 A incident neutrons. Scattered neutrons were observed in energy gain using a time-of-flight method and corrected for the form factor and a detailed balance factor (Windsor 1966). The broken line at small energies shows the calculated extent of the incoherent elastic peak.
predicted by diffusion theory. A check on accuracy is provided by the fact that its area and root-mean-square energy width come within 2% of the exact values calculated using de Gennes' theory of the moments. of the computed curve differs from the Gaussian proposed by de Gennes in being appreciably more peaked at small energies, a region where the moment calculations are not sensitive. Figure 2 also shows neutron scattering data from polycrystalline RbMnF3 (Windsor 1966), a salt whose magnetic properties correspond closely to the present Hamiltonian (Teaney et al. 1962, Windsor and Stevenson 1966). It is seen that a good fit can be obtained with an exchange interaction J/k = 3.2 ±
0.02 0K, not significantly different from that deduced previously from the best-fitting Gaussian.
Acknowledgments
The author is grateful to E. A. Harris and R. D. Lowde for their help.
References
DE GENNES, P. G., 1958, J. Phys. Chem. Solids, 4, 223-6.
HARRIS, E. A., 1964, Phys. Rev. Letters, 13, 158-60.
TEANEY, D. T., FREISER, M. J., and STEVENSON, R. W. H., 1962, Phys. Rev. Letters, 9, 212-4.
WINDSOR, C. G., 1966, Proc. Phys. Soc., 89, 825-31.
WINDSOR, C. G., and STEVENSON, R. W. H., 1966, Proc. Phys. Soc., 87, 501-4.


