PROC. PHYS. SOC., 1966, VOL. 87
Spin waves in RbMnF3
C. G. WINDSOR1 and R.W.H. STEVENSON2
1Solid State Physics Division, Atomic Energy Research Establishment, Harwell, Didcot, Berks.
2Department of Natural Philosophy, Aberdeen University, Aberdeen
MS. received 12th October 1965
Abstract. The spin-wave dispersion relations for the simple cubic antiferromagnet RbMnF3 have been determined at 4.2 oK by inelastic neutron scattering. Spin-wave theory is used to interpret the results in terms of the exchange interactions 2JijSi.Sj between first, second and third neighbours with
The results also confirm that the anisotropy field is less than 400 gauss. The above value of J1 is compared with other experimental results, and with values calculated from the Neel temperature. Good agreement suggests that RbMnF3 is one of the simplest magnetic salts
1. Introduction
The spin-wave dispersion relations of a magnetic salt can be found by observing inelastic scattering collisions in which some of the energy and momentum of an incident neutron is used in exciting a spin wave. If these measurements are performed at low temperatures, when spin-wave theory is applicable, the exchange interactions between the magnetic ions may be deduced from the spin-wave energies.
The salt RbMnF3 has the cubic perovskite structure in which the manganese ions lie on a simple cubic lattice. The lattice constant was redetermined using X rays and found to have the value ao = 4.2396 ± 0.0002 A at room temperature. Below 82 oK the salt becomes antiferromagnetic with the spin directions alternating along cube edges. RbMnF3 is of particular interest in that, unlike many magnetic salts of cubic symmetry, there is no measurable distortion of the lattice in the antiferromagnetic state.
The ordering structure determines the periodicity of the spin-wave dispersion relations in reciprocal space. Figure 1 shows the 110 plane of the reciprocal lattice of a simple cubic antiferromagnet. Nuclear reflection points (all indices integral) are determined by the chemical cell and lie on a simple cubic lattice of side 2p/ao. Magnetic reflection points (all indices half-integral) are determined by the magnetic unit cell and occupy the corresponding body-centred positions. The Brillouin zones defining the symmetry of the spin-wave dispersion relations are found by drawing perpendicular bisectors between adjacent lattice points. In three dimensions the zones are truncated octahedra.
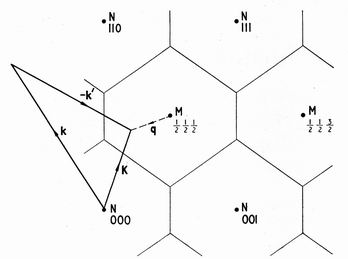
Figure 1. The reciprocal lattice diagram of a simple cubic antiferromagnet in a 110 plane. N and M mark the elastic nuclear and magnetic reflection points. The thin lines show the corresponding zone boundaries. Heavy lines show a possible neutron-scattering diagram for the experimental settings used, k and k' represent the incident and scattered neutron wave vectors. K represents the wave vector transfer k — k', while q represents the transfer relative to the centre of the zone.
2. Experimental details
The experiments were performed on the twin-rotor neutron chopper described by Dyer and Low (1961). This instrument uses mechanical velocity selection and a time-of-flight method to determine the incident and scattered neutron momentum vectors respectively. The energy Eq needed to excite a spin wave vector q is then found using the energy and momentum conservation laws. Incident neutron energies corresponding to 105 oK (3.00 A) and 170 oK (2.34 A) were used.
The sample used in these experiments was a single crystal of volume 0.2 cm3 which was cut from a multicrystal grown by the Stockbarger method. The crystal was mounted in a helium cryostat and aligned so that spin waves propagating in a 110 plane were observed. The counter and crystal angles were then set so that the neutron wave vector transfer K lay in the (1/2,1/2,1/2) zone, as shown in figure 1. The spin-wave intensity decreases away from the magnetic reflection point at the centre of the zone. Near the zone boundary 24-hour runs gave just observable intensities. Spin-wave peaks with a statistical probability less than 2.8 standard deviations were rejected.
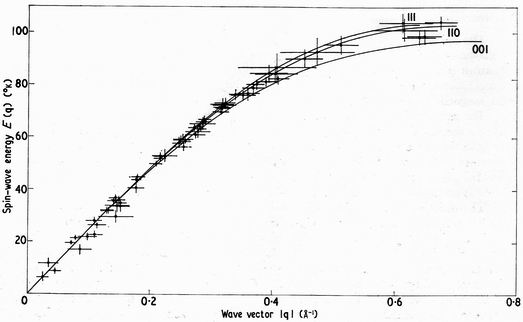
Figure 2. Spin waves in RbMnF3 at 4.2 oK with q vectors distributed over a 110 plane. The smooth curves show the calculated dispersion along particular directions with J1=3.4 ±0.3 o, J2=J3=0.0 oK. These values were found from a least-squares analysis, the exact direction of all the q vectors being taken into account. The fact that the linear part of the curve extends so close to the origin reflects the very small anisotropy field.
3. Results
Figure 2 shows spin waves with q vectors distributed over the 110 plane. Spin-wave theory predicts that the dispersion curve depends on the exchange interactions 2JijSiSj between first, second and third neighbours, and the anisotropy field Ha according to
Eq = [{gbHa + 2S(6J1-12J2 + 8J3) + 4SJ2B}2 -{ 4SJ1A + 4SJ3C}2]1/2
where
B= cos (qx + qy)a0 + cos (qx - qy)a0 + cos (qy + qz)a0+ cos (qy - qz)a0 + cos (qz + qx)a0+ cos (qz - qx)a0
C= cos (qx + qy+ qz)a0 + cos (qx - qy- qz)a0 + cos (qx + qy- qz)a0 + cos (qx - qy- qz)a0.
Here S is the spin on each ion and a0 is the lattice constant of the chemical cell. The theory of spin-wave interactions (Oguchi 1960) predicts that these energies should be increased by the factor (1+0.097/2S) or 1.02. However, this part of the theory has yet to receive any experimental verification. A least-squares fit to the data taking into account the exact direction of all the q vectors gave the following parameters:
Experimental standard errors are quoted. The figures may also be affected by any biquadratic term -2jij(SiSj)2 in the exchange Hamiltonian which would reduce the results by a factor l + 2S2j/J (Harris and Owen 1963). The very small value of the energy intercept at q = 0 reflects the fact that the anisotropy field is very small. The antiferro-magnetic resonance results of Teaney et al. (1962) showed this to be only 4.5 gauss, and our experiments confirm that it is less than 400 gauss. This low value is a consequence of the cubic symmetry giving a vanishing dipolar field.
4. Paramagnetic scattering results
Following the above studies, paramagnetic neutron scattering experiments have been performed using the same instrument, but with a larger poly crystalline sample kept at room temperature (T/TN = 3.7). The exchange interaction causes the scattered neutrons to have an energy spread approximating to a Gaussian distribution (de Gennes 1958). With the assumption that J22 << J12, measurements of the width of this distribution give the exchange interaction J1 = 3.2 ±0.3 oK. Full details will be published elsewhere.
5. Discussion
The spin-wave results show that the bulk properties of RbMnF3 may be interpreted on the basis of a single nearest-neighbour exchange interaction. This confirms the paramagnetic resonance results of Windsor (1963, D.Phil. Thesis, Oxford University), which showed that for Mn2+ pairs in the isomorphous diamagnetic salt KMgF3 the ratio J2/J1 was 0.01 ±0.006. The table shows the present experimental value of J1 compared with other experimental values, and with values calculated from a Neel temperature of 82.6 oK (Moruzzi and Teaney 1964).
| Method | J1 (0K) | Reference |
| Spin waves (4.2 oK) | 3.4 ±0.3 | Present work |
| Paramagnetic scattering (300 oK) | 3.2 ±0.5 | Present work |
| High temperature susceptibility | 3.3 ±0.4 | Walker 1966 |
| Antiferromagnetic resonance | 4.0 | Teaney et al. 1962 |
| --- | 3.7 | Freiser et al. 1963 |
| From TN (green's function) | 3.5 | Oguchi and Honma 1963 |
| From TN (BPW method) | 3.7 | Brown and Luttinger 1955 |
The good agreement suggests that biquadratic exchange effects are not of great importance in this salt. RbMnF3 thus appears to be one of the simplest of magnetic salts.
Acknowledgments
It is a pleasure to acknowledge discussions with M. F. Collins, R. D. Lowde and M. B. Walker. The experimental assistance of N. S. Clark, D. M. Rushton, A. T. Slater and S. A. Wilson was equally valuable.
References
BROWN, H. A., and LUTTINGER, J. M., 1955, Phys. Rev., 100, 685-92.
DYER, R. F., and Low, G. C. E., 1961, Inelastic Scattering of Neutrons in Liquids and Solids
(Vienna: International Atomic Energy Agency), pp. 179-94.
FREISER, M. J., SEIDEN, P. E., and TEANEY, D. T., 1963, Phys. Rev. Letters, 10, 293-4.
DE GENNES, P. G., 1958, J. Phys. Chem. Solids, 4, 223-6.
HARRIS, E. A., and OWEN, J., 1963, Phys. Rev. Letters, 11, 9-10.
MORUZZI, V. L., and TEANEY, D. T., 1964, Bull. Amer. Phys. Soc., 9, 225.
OGUCHI, T., I960, Phys. Rev., 117, 117-23.
OGUCHI, T., and HONMA, A., 1963, /. Appl. Phys., 34, 1153-60.
TEANEY, D. T., FREISER, M. J., and STEVENSON, R. W. H., 1962, Phys. Rev. Letters, 9, 212-4.
WALKER, M. B., 1966, Proc. Phys. Soc., 87,45-8.