
INSIGHT, 41, 372-375, 1999.
Turning surface radar scans into three-dimensional buried mine positions
Colin Windsor*, Lorenzo Capineri and Francesco di Zinno
Department of Electronic Engineering, University of Florence, Via S. Marta 3, 50139 Florence, Italy; *and 21, Blackwater Way, Didcot, OX11 7RL, UK
Abstract- A method is presented for the rapid evaluation of buried object positions in three dimensions from sets of ground penetrating radar (GPR) range measurements. The "ringing" signal from the reflected object in any one scan is correlated with that of its neighbours to produce a set of range values. Randomly chosen sets of three range values are then used to solve analytically for the three co-ordinates of the mine position. A three-dimensional plot of the results is developed to give an intuitive image of the estimated buried object position and the relative uncertainty. The method is demonstrated using measurements recorded and made available by the DeTeC group at EPFL, Lausanne, Switzerland. The depth of a typical anti-personnel land mine buried at 100 mm nominal depth in sand is evaluated to around 25 mm accuracy and it position to around 30 mm.

Keywords: mine detection; radar;GPR
1. Introduction
There is a clear need for rapid evaluation of the complex data patterns produced by ground penetrating radar (GPR) when used for the detection of buried anti-personnel mines. A review of the GPR method has been given by Daniels [1]. The problems of using GPR for the exacting task of detecting anti-personnel mines in the field have been reviewed in the Proceedings of the SusDem'97 Conference held in Zagreb in 1997 [2]. The signal reflected from the mine at any given sensor position generally has several superposed "ringing" waveforms reflected from the ground surface, from the mine, and from other scattering centres such as rocks, tree roots, bottle tops, or shrapnel. A scan recorded as a function of sensor position, as in the "B-scan" of figure 1, shows a nearly constant range for the ground surface, and a characteristic hyperbolic arc from the scattering centre indicating the changing range to the object as the sensor is moved. to
Fig. 1. The Ground Penetrating Radar (GPR) signal reflected from an anti-personnel mine buried in sand, recorded as a function of probe position, and elapsed time from the initial radar pulse. The grey scale image is fitted to the dynamic range of the reflected radar signal to form the B-scan of ultrasonic studies. The strong signal at nearly constant time is from the sand surface, the arc-like signal shows the changing range of the mine
across the scan. The black circles show the results of the "correlation following" method described later, and the black curved line shows the calculated signal deduced from the three-dimensional position of the mine as found by the method.
Such patterns can be analysed to show the position along the scan of nearest approach to the object, but many such B-scans, taken along different sensor paths, must be analysed
to determine the defect position in three-dimensions. The evaluation of such complex
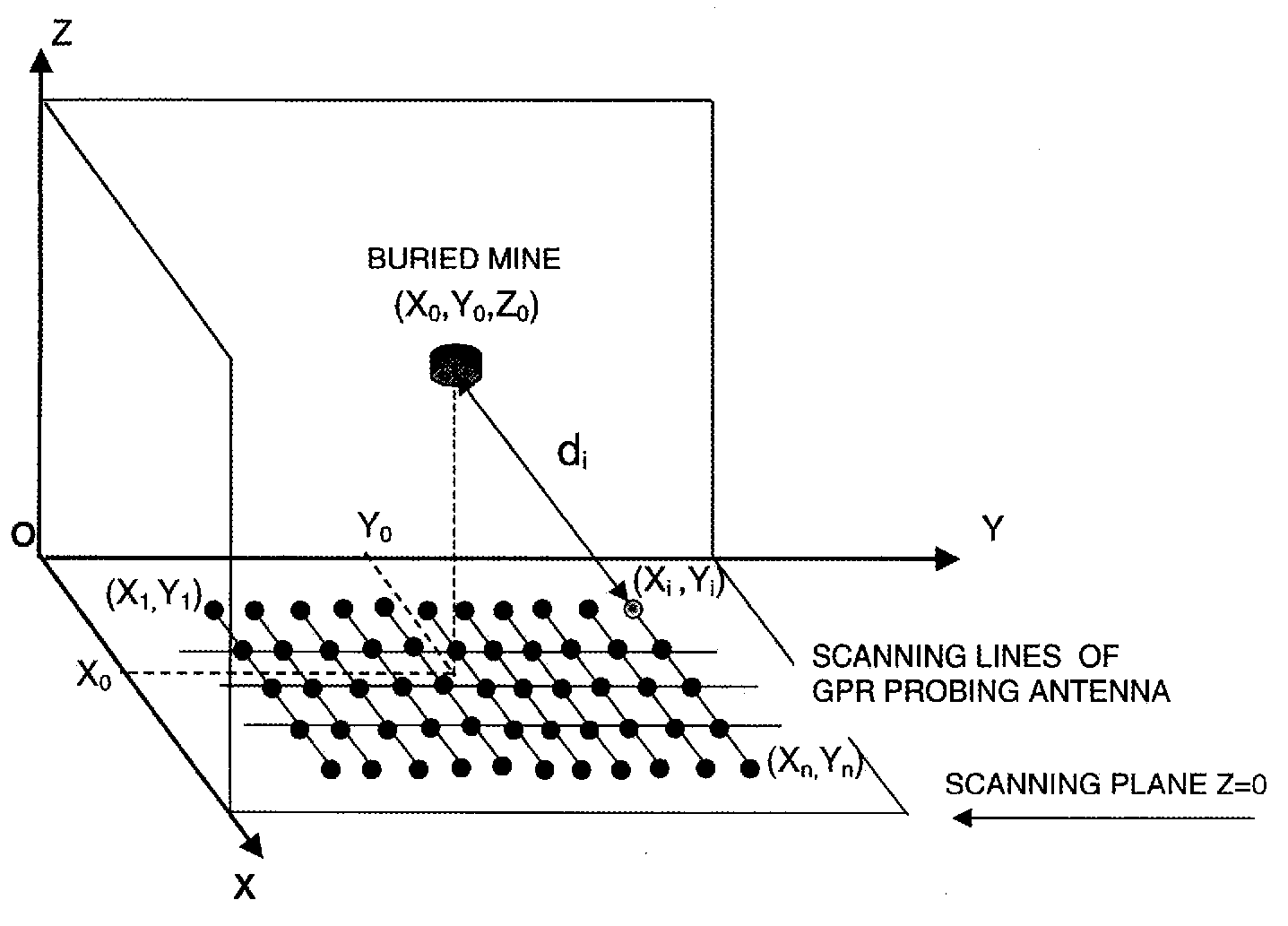
sets of scans requires great skill, since the patterns from several displays need to be assimilated. The problem is even more difficult in practice since the scans are frequently performed not as a simple raster along two orthogonal directions, as shown for example in figure 2, but as a polar scan as a function of radius and angle from a given point, as a continuous scan produced for example by an oscillating arm travelling at a constant speed. To analyse such generalised scans requires the correlation of the signals between a given point (xi,yi) with a series of points (xj,yj) over the raster satisfying the condition that | (xi,yi) - (xj,yj)| lies within the range of the signal from the object to be found.
2. Theory
Suppose the transmitted GPR pulse may be assumed to be a sharp delta-function at a time t=0. The reflected pulse, recorded as a function of the time of flight ttof is then measured to form the "A-scan" of ultrasonics notation A(ttof ). For a point-like object at a position (xo,yo,zo) the reflected signal will be centred on a time
ttof(xi,yi) = to+ 2Ö [ (xi - xo)2 + (yi - yo)2 + zo2 ]/v (1)
depending on the velocity v of the radar pulse in the medium and the constant known time to of the signal reflected from the front surface of the medium. If these two constants are known, the time-of-flight signal may be immediately transformed into a range distance signal di(xi,yi) such that
di(xi,yi) = ( ttof(xi,yi) - to )/2v
= Ö [ (xi - xo)2 + (yi - yo)2 + zo2 ] (2)

Fig. 2. A possible raster scan for a Ground Penetrating Radar source over a buried object at position (xo,yo,zo). The scan may be analysed into a series of range measurements giving the distance di as a function of a series of n positions (xi,yi) (i=1,n) of the sensor within the plane. In this figure the Z axis represents the depth coordinate.
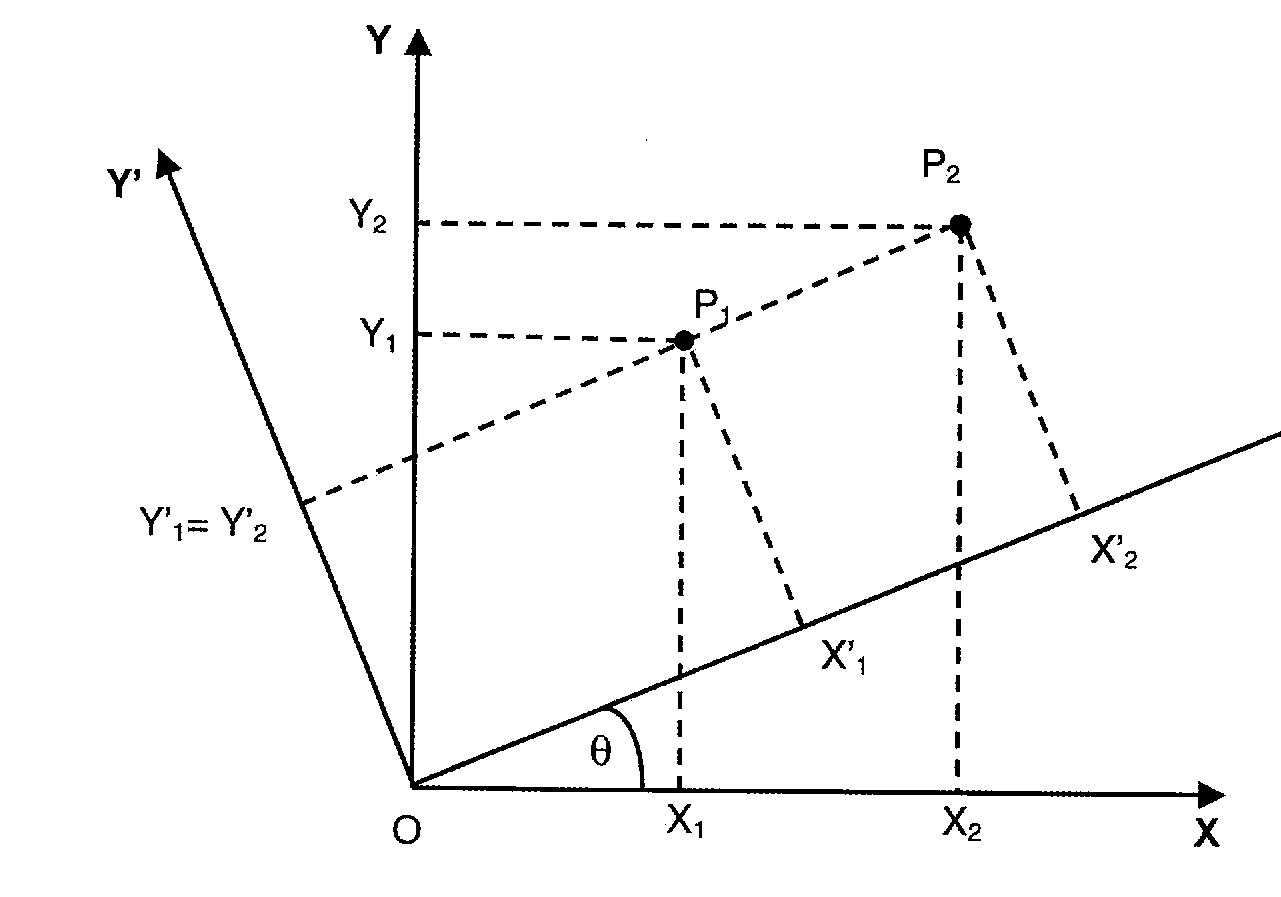
In principle any three range signals with indices i1, i2 and i3 can be used to solve for the three unknowns xo, yo and zo. For this three-dimensional case, the three quadratic equations can be reduced to linear equations by a rotation of axes in the xy plane. The first step is to subtract the expressions for d12 from that of d22for giving
d22 - d12 = x22 - x12 -2(x2 - x1)xo + y22 - y12 -2(y2 - y1)yo (3)
Fig. 3. The rotation of axes in the xy plane which enables two of the three selected positions (xi,yi) with i=1 and i=2 to become points (xi',yi') such that y1' = y2', and so enable the equation for xo' to be solved from a linear equation.
The terms involving y vanish in the special case when the points i2 and i1 lie parallel to the x axis so that y2 = y1. However even for
tanq = (y2 - y1)/( x2 - x1) (4)
the general case, the axes x and y may be rotated by an angle q as shown in figure 3, so that with respect to the transformed axes x', y' we have y2' = y1'. This occurs when
The equations for the transformed variables are then
xi' = xi cosq + yi sinq ;
yi' = - xi sinq + yi cosq . (5)
Equation 3 then becomes in the transformed co-ordinates system
d22 - d12 = x2'2 - x1'2 -2(x2' - x1')xo', (6)
from which xo' is given by
xo' = 0.5( d22 - d12 - x2'2 + x1'2 )/(x1' - x2'). (7)
It is now possible to use the analogue of equation 3 with points i3 and i1 to give the following expression for yo'
yo' = 0.5( d32 - d12 + (x1' - xo')2
- (x3' - xo')2 + y1'2 - y3'2)/(y1' - y3') (8)
Having found xo' and yo' it is a simple matter to substitute in equation 2 with point i1 to give the following value for zo
zo = Ö [ d12 - (x1' - xo')2 - (y1' - yo')2 ]. (9)
In practice many choices of the three di(xi,yi) with i=i1, i2 and i3, may not correspond to any real object position (xo,yo,zo), give a negative square root argument and should be abandoned.
The true object position in the original co-ordinate system may now be evaluated from the inverse equations 5
xo = xo'cosq - yo'sinq ;
yo = xo'sinq + yo'cosq . (10)
2. The "correlation follow" method applied to a land mine buried in sand
GPR scans from commonly found land mines buried in sand or soil have been collected by the DeTeC team at EPFL Lausanne Switzerland and have been made freely available [3]. Here we consider just one set of scans from a mine (type PFM) buried in sand at a nominal depth of 100mm.
The data acquisition used was a SPRscan from ERA Ltd., equipped with one 1 GHz antenna.
The scans take the form of two sets of raster scans along the X and Y axes over the mine as illustrated in figure 2. Figure 1 gave an example scan showing a clear reflection from the mine without complications from other significant reflectors. The series consists of 21 B-scans along both the X and Y directions with at least some indication from the mine. The reflections from the mine in many of the scans can be correlated together so that the set of scans is particularly suited to demonstrate the present method. Later papers will describe more complex GPR scans including several overlapping arcs which could also be analysed, in principle, using the present method.
The "correlation follow" method has been recently described by Windsor and Capineri [4], and is used unchanged for the first stage of the analysis of each B-scan. The process of arc extraction can commence on any B-scan with a strong signal, by performing a search over the whole recorded scan below the strong surface reflection, for the position of maximum signal change. This position, defines a particular phase position within the ringing signal which will be maintained throughout the arc-extraction process.
The method searches the hyperbolic arc points following the maximum correlation between consecutive signals (A-scans) over a defined correlation window. When two arcs intersect or when the signal to noise ratio is low, the correlation becomes poor and the method attempts to recover this situation searching forward for a good correlation with signals relative to further lateral probe positions. During this search the correlation window is always placed on the direction calculated with an average local gradient. An average gradient can be calculated at each step with the last m points of the arc. This momentum term in the gradient, resulted effective to solve critical situations for arc extraction that otherwise could have led to premature end of the search or wrong search directions. The search methods ends when the signal to noise ratio is below a defined threshold or when all the allowed attempts failed to find a good correlation [5].
4. Three-dimensional visualisation of results.
A test set of images was obtained by the DeTeC project [3]: the mine type PFM series of images was downloaded and processed from that database. The mine, a small air-delivered plastic anti-personnel mine with low metallic signature, was buried in a tank box filled with sand (estimated phase velocity 1.5*108 m/s) at four different depths: 10mm, 30mm, 50mm and 100mm.
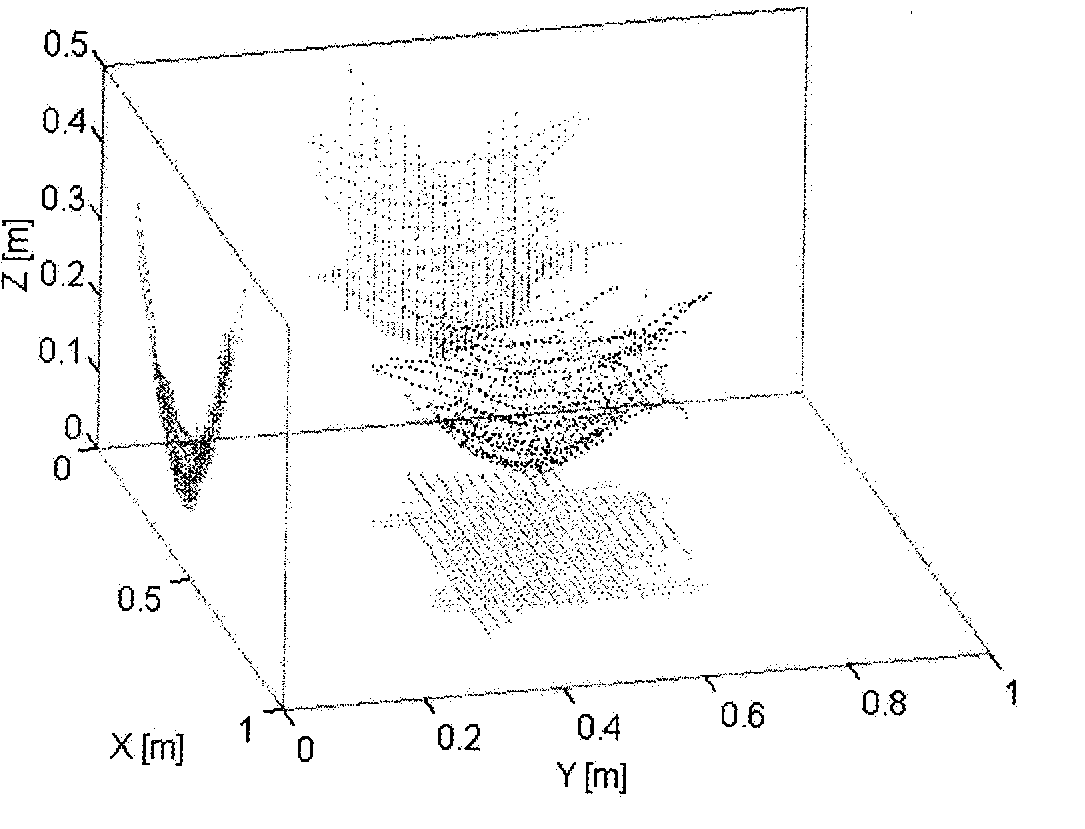
Fig. 4. Three-dimensional plot of extracted arcs from the data set of B-scan images for the buried mine in sand (type PFM). The projection on the cardinal planes are displayed together with the extracted arcs. Arcs points in black; projected points in grey.
In the following three-dimensional plots, the reference system of figure 1 was rotated to provide a more clear view of results. It can be observed that the ensemble of arcs is enveloped by an hyperbolic surface as predicted by the equation (1) of time of flight. The minimum of this surface corresponds to the lowest depth detected for the buried object. The regularity of the extracted arcs according to equation (1) can be easily checked in a quantitative and rapid way by the arcs' projections on Y-Z, X-Y and X-Z planes
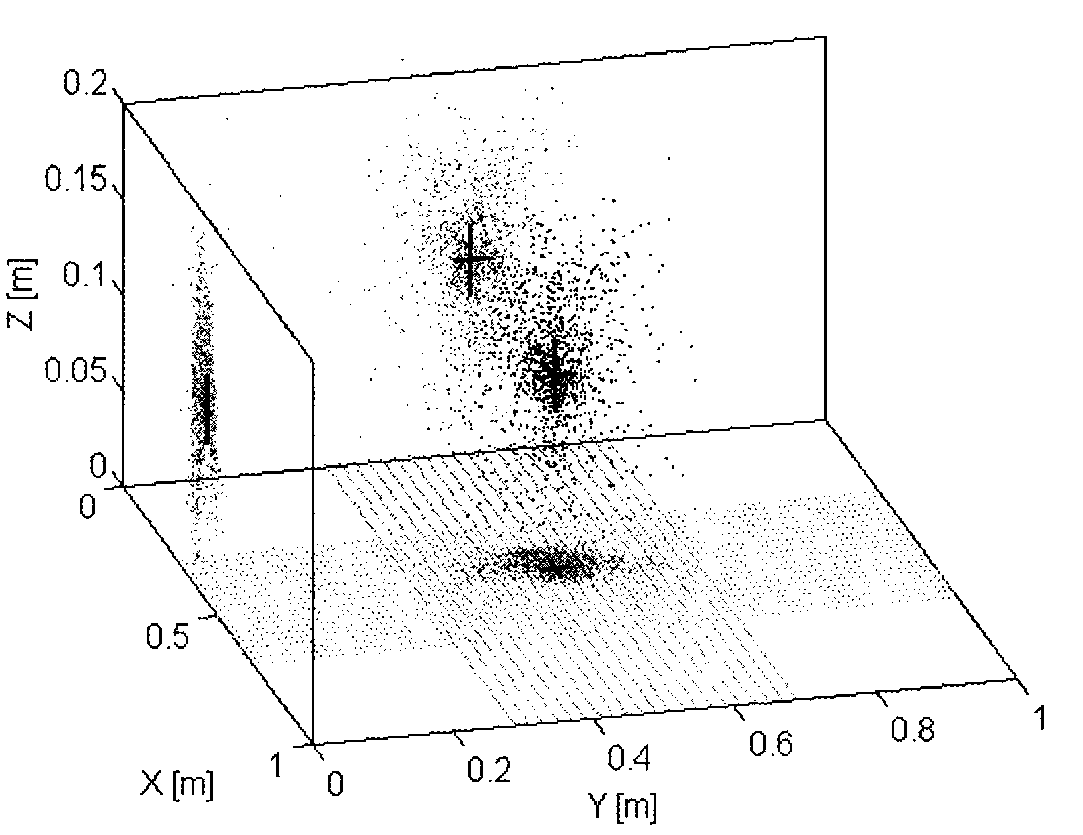
The estimation of the buried object position is performed using this data set of points according to the inversion process described in section 2. For each triplet of points selected at random a possible object position is found. These positions are accumulated in a course of 3-dimensional accumulator space matrix and the process terminates when a maximum value is reached in any one cell of the accumulator. The centre of gravity of the points distribution in the accumulator is estimated and assumed to be the most likely object position. At the same time an associative accumulator is incremented detailing the coordinates of the possible object position. The accumulator contains floating points values in order to avoid the problem of X,Y and Z coordinates quantization. The points in the associative store can be displayed in real coordinates as shown with black points in Figure 5. The position of centre of gravity corresponding to the mine position is outlined by a 3d cross in Figure 6. In order to evaluate the accuracy of the positional estimates by eye, the variances of this distribution are presented as the projections of the points in gray color over the three cardinal planes. Moreover the length of the segments forming the 3d cross are equal to twice the standard deviation of the distributions. The set of 21 orthogonal lines on the scanning plane Z=0 in Figure 6 is a useful spatial reference for the determination of the X-Y coordinates of the buried object with respect to the raster scan with the GPR probe. The method was also tested with images from the same mine at smaller nominal depths. The results obtained by the automatic processing algorithm for each nominal depth (10mm, 30mm, 50mm and 100mm) are summarised in Table 1. For each image the buried mine centre of gravity is reported together with the relative standard deviations. The images were all similar to the example shown in figure 1 in terms of signal to noise ratio, size and resolution. Two observations can be made on these preliminary results. Fi rstly, the standard
Fig. 5. Estimates of the position of the buried mine, at the final stage of the inversion process. The points within the accumulator space are displayed in black in real coordinates x,y,z. The z axis corresponds to depth, the x and y axes correspond to the GPR probe position within the plane of the scan. The centre of gravity of the spatial position is displayed as a three-dimensional (3d) cross. The projections of the distribution on the cardinal planes are displayed with grey points together with the centre of gravity position. The points have different weight but here are all displayed in black colour. The 3d cross position corresponds to the estimated buried object position and the spread of the distribution provides a qualitative information of the estimate uncertainty. In this case depth of the mine was estimated at the position xyz=(0.430,0.49,0.105)m with standard deviations (0.029,0.025,0.023)m.
Each set of measures consists of 21 B-scans on the X-direction and 21 B-scans on the Y-direction. The scan length of the radar probe is 1 meter, the distance between two parallel scans is 20mm. The collection of hyperbolic arcs extracted from images corresponding to a nominal mine depth of 100m, can be displayed with a three-dimensional plot, as shown in Figure 4.
deviation of the depth (z-coordinate) in generally better than that of the x or y coordinates. This can be explained by the improved depth resolution given by our retention of the phase information in the back-scattered signal. It is easy to achieve values that are a small fraction of the wavelength calculated at the central frequency of 1GHz (l = v/f=1.5 108 / 1 109 = 150 mm). Secondly the standard deviation of the depth estimate appears to worsen with deeper objects. This is probably due to the increased attenuation by the medium. The depth estimate at very short nominal depths, such as 10mm, appears to suffer from large systematic errors. This is probably caused by the strong interference between the reflected signals from the different surfaces of the mine, and from the air-sand interface.
Table 1. The estimated position of a mine buried at different nominal depths in a sand box, from the original GPR images using the new method.
|
|
Nominal depth z=10mm |
||
|
|
x |
Y |
z |
|
Centre of gravity [mm] |
451 |
451 |
23 |
|
Standard deviation [mm] |
29 |
32 |
12 |
|
|
Nominal depth z=30mm |
||
|
|
X |
Y |
z |
|
Centre of gravity [mm] |
430 |
460 |
36 |
|
Standard deviation [mm] |
23 |
28 |
18 |
|
|
Nominal depth z=50mm |
||
|
|
x |
Y |
z |
|
Centre of gravity [mm] |
414 |
479 |
42 |
|
Standard deviation [mm] |
23 |
29 |
18 |
|
|
Nominal depth z=100mm |
||
|
|
x |
Y |
z |
|
Centre of gravity [mm] |
430 |
499 |
105 |
|
Standard deviation [mm] |
29 |
25 |
23 |
Conclusions.
An algorithm has been developed to estimate the position of buried objects by processing three-dimensional data sets formed with GPR images. The main characteristics of the algorithm are:
1) independence from any particular GPR probe scanning method: suitability for test data taken at arbitrary probe positions
2) ability to correlate data from many scans, and so produce
a three-dimensional object position estimate
3) ability to estimate the probable error in the object position
4) ability to work with little operator intervention
5) fast processing speed
The algorithm has been tested on three-dimensional raster data collected using laboratory GPR by the DeTeC project for humanitarian demining [3]. The results show that a single buried landmine in a sandbox can be accurately detected within the depth range from 20 to 100 mm with an uncertainty better that 30mm. The present promising results obtained using this method will be extended by analysing further GPR images acquired in more realistic conditions. These need to include the use of real soil containing rocks, and the detection of the mine in the presence of other small metallic objects likely to be present in a minefield.
Acknowledgements.
This work was supported with the scientist mobility program of the University of Florence, Italy. We wish also to thank Prof. J.D. Nicoud at LAMI DeTec at Ecole' Polytechnique Lausanne, Switzerland.
References
[1] Daniels D J, Surface penetrating radar for industrial and security applications, Microwave Journal, December 1994, pp 68-82
[2] SusDem'97 International Workshop on Sustainable Humanitarian Demining
Zagreb, Croatia, Sept 29 - Oct 1, 1997, http://diwww.epfl.ch/w3lami/detec/susdem.html
[3] Contact Prof. J-D Nicoud at LAMI-DeTeC , Swiss Federal Institute of Technology, IN-F Ecublens, CH-1015, Lausanne, Switzerland, Internet address: http://diwww.epfl.ch/w3lami/detec/gprsoft.html.
[4] C.G. Windsor, L. Capineri, Automated object Positioning from Ground Penetrating Radar Images, INSIGHT, Journal of the British Institute of Non Destructive Testing, Vol. 40, N.7, July 1998, pp.482-488
[5] L. Capineri, C.G. Windsor and F di Zinno Three Dimensional buried mine positions from arbitary radar surface scans INSIGHT, Journal of the British Institute of Non Destructive Testing, Vol. 41, N.6, June 1999, pp.372-375